Infinitely Close or Perfectly Equal? Why 0.999... = 1

A Journey Through Infinite Series and Their Surprising Results

This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.

---

Some weeks ago we explored infinity through the The Impossible Race. The key takeaway was: it is possible to add an infinite number of things yet get a finite result.

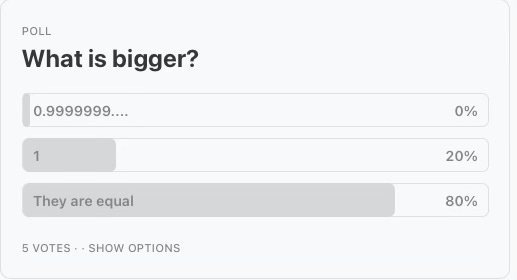
I ended that post with a question, which I also asked on a separate poll on Instagram:

The results revealed two interesting insights:

1. People understand that 0.999… is at most 1 (which makes intuitive sense: 0.999... starts with 0, while 1 starts with 1)

2. Many people are uncertain about what 0.999... precisely means: is it equal to 1 or slightly smaller?

Let's Make Sense of 0.999...

The number 0.999… can be written as an infinite sum:

\(0.9999... = 0.9 + 0.09 + 0.009 + \dots \)

Why is this useful?

Instead of dealing with 0.999..., a concept we might find confusing, we now have a sum of infinite terms where we understand each individual piece.

We still have to figure out what an infinite sum really means, but at least we know the components that make it up.

Two Key Insights

1. If I stop the infinite sum at any finite point, the result will be less than 1.
   Whether it's 0.9, 0.99, 0.999, or 0.9 followed by a million 9s—as long as the number of 9s is finite, the result remains less than 1.

2. I can get as close to 1 as I want by adding sufficiently many terms.
   Want to be within 0.00000001 of 1? Just calculate up to 0.99999999. Need even more precision, like 0.000000000000001? Then calculate up to 0.999999999999999.

Let's visualize these two statements:¹

1. Stopping the sum at any given point (the green points below) gives something smaller than 1:

2. Given any maximum tolerance (the orange line below), we can get closer to 1 than that by adding sufficiently many terms:

Why 0.9999… = 1

Now we can make a compelling argument that 0.999... must be equal to 1, not smaller.

Take any number smaller than 1, say 0.999999876. We've established that by considering sufficiently many terms in our infinite sum, we can get closer to 1 than this number (for example, 0.9999999 is closer to 1 than 0.999999876). Our infinite sum 0.999... is larger than 0.9999999 (it's 0.9999999 plus something else), so it must also be larger than 0.999999876.

Therefore:

Given any number smaller than 1, the number 0.999… is larger than that number.

If 0.999... is larger than every number smaller than 1, and it's not larger than 1, then it can only be equal to 1!

If this is still troubling to you, think again about The Impossible Race. Just as Achilles eventually catches the tortoise despite being behind the tortoise at every step in the paradox, 0.999... equals 1 despite 0.9999999 being smaller than 1 for any finite number of 9’s.

Real-Life Applications of Infinite Sums

This concept isn't just mathematical curiosity—it has several practical applications:

1. Computer Graphics: When rendering realistic 3D images, computers use infinite series approximations to calculate lighting and reflections. By adding more terms, the image becomes more realistic, but at some point, adding more terms makes no visible difference—similar to how 0.99999999, with sufficiently many 9’s, is practically indistinguishable from 1.

2. Financial Calculations: When calculating compound interest over many periods, the formula involves a sum that approaches a limit. Understanding convergent series helps financial analysts make accurate long-term predictions.

3. Signal Processing: When your smartphone processes audio or your streaming service compresses video, they use mathematical techniques based on infinite series to approximate complex waveforms efficiently.

Why This Matters

Understanding that 0.999... = 1 helps us grasp a fundamental concept in mathematics: limits.

A limit describes the value a function or sequence approaches as it extends toward infinity. This concept underlies calculus, which powers everything from rocket science to economic modelling.

It also teaches us something profound about infinity itself. Our intuition often fails when dealing with the infinite—what seems "obvious" (that 0.999... should be less than 1) turns out to be incorrect when we apply rigorous mathematical thinking.

A Final Thought

Mathematics often challenges our intuition, pushing us to think beyond what seems immediately obvious. The equality 0.999... = 1 reminds us that rigorous mathematical reasoning sometimes leads to conclusions that initially feel wrong but reveal deeper truths about numbers and infinity.

What other mathematical concepts do you find counterintuitive? Let me know in the comments!

In case you missed it

• The Linda Problem: When Our Brain Tricks Us Into The Impossible

• The Hidden Psychology of Change: How We Value Gains and Losses

• Bitcoin 101: The Secret Power Behind Decentralized Electronic Money

• Bitcoin 201: Why It Compares to Gold & What Happens in 2140

What do you want next?

1. These plots were made using a different infinite sum that approaches 1.