The Impossible Race: How a Tortoise Challenged Mathematics for 2,500 Years
Infinite Steps, Finite Distance: The Mathematical Puzzle That Stumped Philosophers
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Sometimes the most logical reasoning leads to the most impossible conclusions.
Zeno of Elea, a Greek philosopher from the 5th century BCE, discovered several paradoxes that have puzzled humanity for over two millennia. His most famous paradox proposes that the great warrior Achilles could never overtake a tortoise in a race if given a head start. His argument breaks movement into infinite steps, preventing Achilles from ever passing the tortoise.
Motion itself appears impossible when viewed through Zeno's logical lens. What goes wrong?
Zeno’s Paradox
Here's a mind-blowing puzzle that has stumped philosophers and mathematicians for millennia:
Zeno’s Paradox
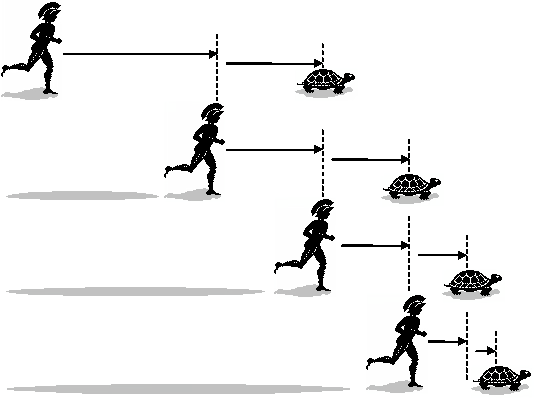
The legendary Greek warrior Achilles agrees to race a tortoise over a 1km race.
Convinced of his superiority, Achilles gives the tortoise a 100-meter head start. Achilles starts at the 0-meter mark, while the tortoise starts at the 100-meter mark.
The race begins! But here's where things get strange...
By the time Achilles reaches the 100-meter mark, the tortoise has moved forward. It hasn't moved far, but it has moved.
Let's say the tortoise reaches the 110-meter mark (meaning Achilles runs 10 times faster than the tortoise).
Now Achilles is at 100 meters, and the tortoise is at 110 meters.
By the time Achilles reaches 110 meters, the tortoise has moved again.
Now Achilles is at 110 meters, and the tortoise is at 111 meters.
When Achilles reaches 111 meters, the tortoise has moved to 111.1 meters.
When Achilles reaches 111.1 meters, the tortoise has inched forward to 111.11 meters.
And so on, infinitely.
The argument seems clear: whenever Achilles reaches the tortoise's previous position, the tortoise will have moved ahead. Since there's always a gap between them, Achilles can never overtake the tortoise.
But this contradicts our everyday experience—faster runners do overtake slower ones. So what's happening?
What do you think about this paradox? Is there a flaw in the reasoning? Share your thoughts in the comments!
First, What is a Paradox?
When the ancient philosopher Diogenes the Cynic heard Zeno's arguments, he said nothing but stood up and walked, in order to demonstrate the falsity of Zeno's conclusions.
But this misses the point of a paradox. A paradox isn't disproven by asserting the obvious ("Of course Achilles will catch the tortoise—he's faster!").
A true paradox presents us with a seemingly valid argument that leads to an impossible conclusion. We know the conclusion must be wrong, but the challenge is finding exactly where the reasoning fails.
Aristotle Takes on the Tortoise
Solving Zeno's Paradox challenged even history's greatest minds. Aristotle described it this way:
In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead.
Aristotle proposed that the key to the paradox lies in how it breaks a finite distance (the 1km race) into infinite pieces (first 100m, then 10m, then 1m, then 0.1m, etc.).
He argued that this infinite division doesn't prevent someone from traversing the distance, since these subdivisions don't actually exist unless something is done to them (in this case stopping at them).
While groundbreaking for its time, Aristotle's solution feels somewhat unsatisfying: "Things don't exist unless something is done to them?" That's a bit too philosophical for a clear answer.
Playing with Infinity
It took nearly two thousand years, until mathematicians like Isaac Newton and Augustin Cauchy, to provide a mathematically rigorous solution to Zeno's paradox.
We've previously explored counter-intuitive properties of infinity using the Infinite Hotel. Solving Zeno’s Paradox requires understanding another counterintuitive property of infinity:
When we add an infinite number of terms, the sum can still be finite.
Let me give you a non-example and an example:
If you add 1 + 1 + 1 + 1 … infinitely, you’ll get infinity.
But if you add 9 + 0.9 + 0.09 + 0.009 + … infinitely, you’ll get 9.999… which is finite (it is at most 10).
What's the crucial difference?
For an infinite sum to be finite, the terms need to become very small, very quickly.
The Solution: Racing Against Time
What does this have to do with Zeno’s Paradox?
Let's analyze the time it takes Achilles to complete each step in the paradox:
First, Achilles runs from 0 to 100 meters. At his speed, this takes 10 seconds.
Total time: 10sNext, Achilles runs from 100 to 110 meters. This takes 1 second.
Total time: 10s + 1s = 11sThen, Achilles runs from 110 to 111 meters. This takes 0.1 seconds.
Total time: 10s + 1s + 0.1s = 11.1sNext, from 111 to 111.1 meters: 0.01 seconds.
Total time: 10s + 1s + 0.1s + 0.01s = 11.11s
If we continue this pattern, the total time for all these infinite steps is:
While Zeno's argument involves infinitely many steps, these steps sum to a finite amount of time—approximately 11.11 seconds. After this finite time, Achilles has indeed overtaken the tortoise!
The Beauty of Infinity
This solution reveals something profound: we can add infinitely many terms and still get something finite. This concept was revolutionary and led to the development of calculus and modern mathematics.
The precise equality between an infinite sum and a finite result is a cornerstone of mathematical analysis.
What does it even mean to add infinite things? Surely 10 + 1 + 0.1 + 0.01 + … = 11.111… is not infinite (for instance, it is a number smaller than 12), but what number is it exactly? In this case, there is an easy way to equate 10 + 1 + 0.1 + … to a specific number, namely 11.111…, which now looks something familiar. But what about something like 1 + 1/2 + 1/4 + 1/8 + … ? What is this equal to, if anything?
Let me end this post with a question for you, which we might discuss on a future post:
In case you missed it
Microsoft’s Quantum Breakthrough: A New State of Matter & Quantum Computing
The Hidden Power of Information: How Small Details Can Change Everything
The Limits of Democracy: What Arrow’s Impossibility Theorem Reveals about Fair Elections
What do you want next?


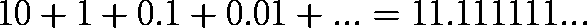
Now that it has a logical explanation, does it continue to be a paradox?.... very interesting as always!!