The Infinite Hotel: Why Infinity is Larger Than You Think

Welcome to the Infinite Hotel: Where There is ALWAYS a Room for You

This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.

---

Designed by Freepik

How big is infinity?

Imagine you arrive to a hotel with an infinite number of rooms. What if I told you that, even if all the rooms are filled, there is still a place for you? What if I told you that, even if all the rooms are filled, there is still a place for infinitely more people?

Today we see that infinity is much larger than we think.

Today in a Nutshell

• The Infinite Hotel is a thought experiment proposed by mathematician David Hilbert to demonstrate the counterintuitive nature of infinite sets.

• In an infinite hotel, even if it is full, you can fit one more person.

• In fact, in an infinite hotel, even if it is full, you can fit infinite more people.

• Things do get worse than this…

The Largest Hotel in the World

The First World Hotel is the largest hotel in the world.

It is located in Malaysia and has an astonishing number of 7,351 rooms. It is a very large hotel, but it has a problem: if its 7,351 rooms are occupied and you arrive to the hotel, you won’t have a place to sleep. It is big, very big. But not enough.

After visiting the hotel and seeing it full, you decide that there needs to be a larger hotel. What happened to you can’t happen to anyone again. So you build a hotel twice as big.

Your hotel can now host 14,702 people! This is a huge hotel. But, again, it has a problem. If its 14,702 rooms are occupied and you arrive to the hotel, you won’t have a place to sleep. Huge hotel, but not enough.

The Infinite Hotel

Let’s imagine we could build an infinite hotel.

It is so big that, no matter what, there will always be a room for you.

For any number that you can imagine, say 10,203,209,300, there is a Room 10,203,209,300. Make it twice as big, there is also a Room 20,406,418,600.

It is so big, that you put a great sign on its door:

Knock knock

Now imagine every single room of your hotel is occupied.

You have a guest in Room 1; another in Room 2; another in Room 3…and so on and so forth.¹

A guest arrives to the hotel. He notices it very busy, lots of people around. But he sees your big sign:

You are the manager of the hotel:

It is an infinite hotel—he must fit in.

But all the rooms are filled—there is no free room.

How do you fit the new guest in?

Think about it for a moment, see if you can come up with something.

The Infinite Hotel

Here is the way to fit your new guest in.

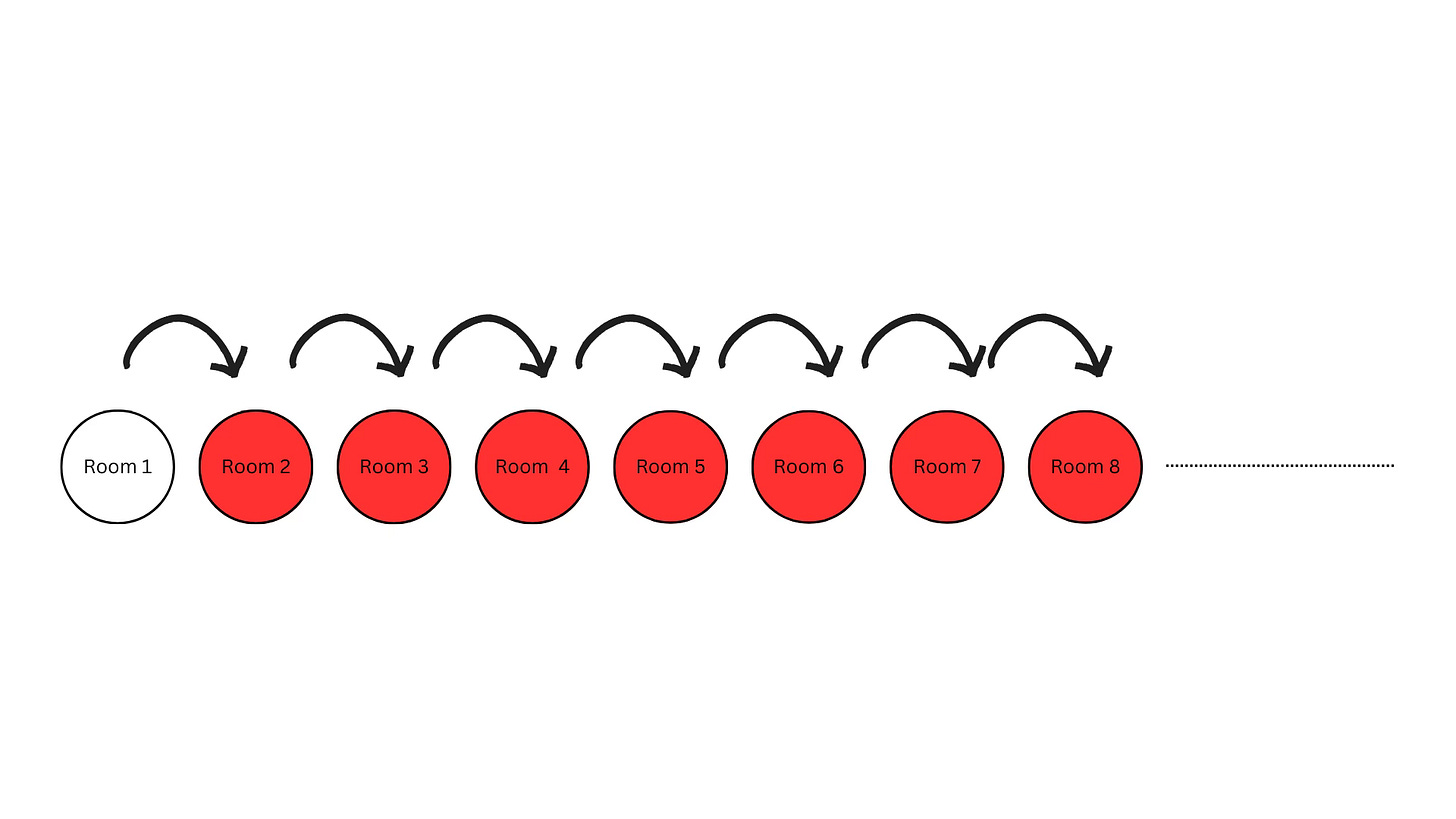
Right now, all rooms are occupied. Let’s picture occupied rooms in red like this:

To fit the new guest, you tell your current guests:

If you are in room 1, move to room 2.
If you are in room 2, move to room 3.
In general, whatever room you are in, move to the next room.

Everyone can move to the next room: the person in Room 1 moves to Room 2, which is now free because that person has moved to Room 3, and so on.

But something else happens:

The first room becomes free!

That is the room for your new guest.

Think about what just happened. Your hotel had infinite rooms, but it also had infinite guests. You wanted one more guest to fit in—and you fit them in. That is, you did something like²

\(\infty + 1 = \infty.\)

This shows a property of infinite that is counterintuitive:

Infinite rooms can fit infinite people and one more.

Note that this does not happen for any finite number: if x + 1 = x, then (cancelling the x) we get an absurdity 0 = 1.

Knock knock, knock knock, knock knock…

With the same trick you can fit 2 more people: just tell everyone to move to 2 rooms further, and you will have rooms 1 and 2 free for the new guests.

You can even fit 100 more people: just tell everyone to move to 100 rooms further.

In fact, given any finite number of people, you can fit them in like this.

But what if infinite people arrive to your hotel?

Imagine your hotel is full, and a bus with infinite people arrives to your door. It brings a lot of people, certainly. But you have a big sign at the door:

You better live to your promise!

Unlike before, you can’t tell your guests “move X rooms further”. Like this you will be able to fit 2, 100, 2,103,450 or 7,848,483,303,393 people. But not infinite people.

What can you do to fit them in?

This is a bit harder than before. Can you come up with any idea?

Designed by Freepik

Here is what you need to tell your guests:

If you are in room 1, move to room 2.
If you are in room 2, move to room 4.
If you are in room 3, move to room 6.
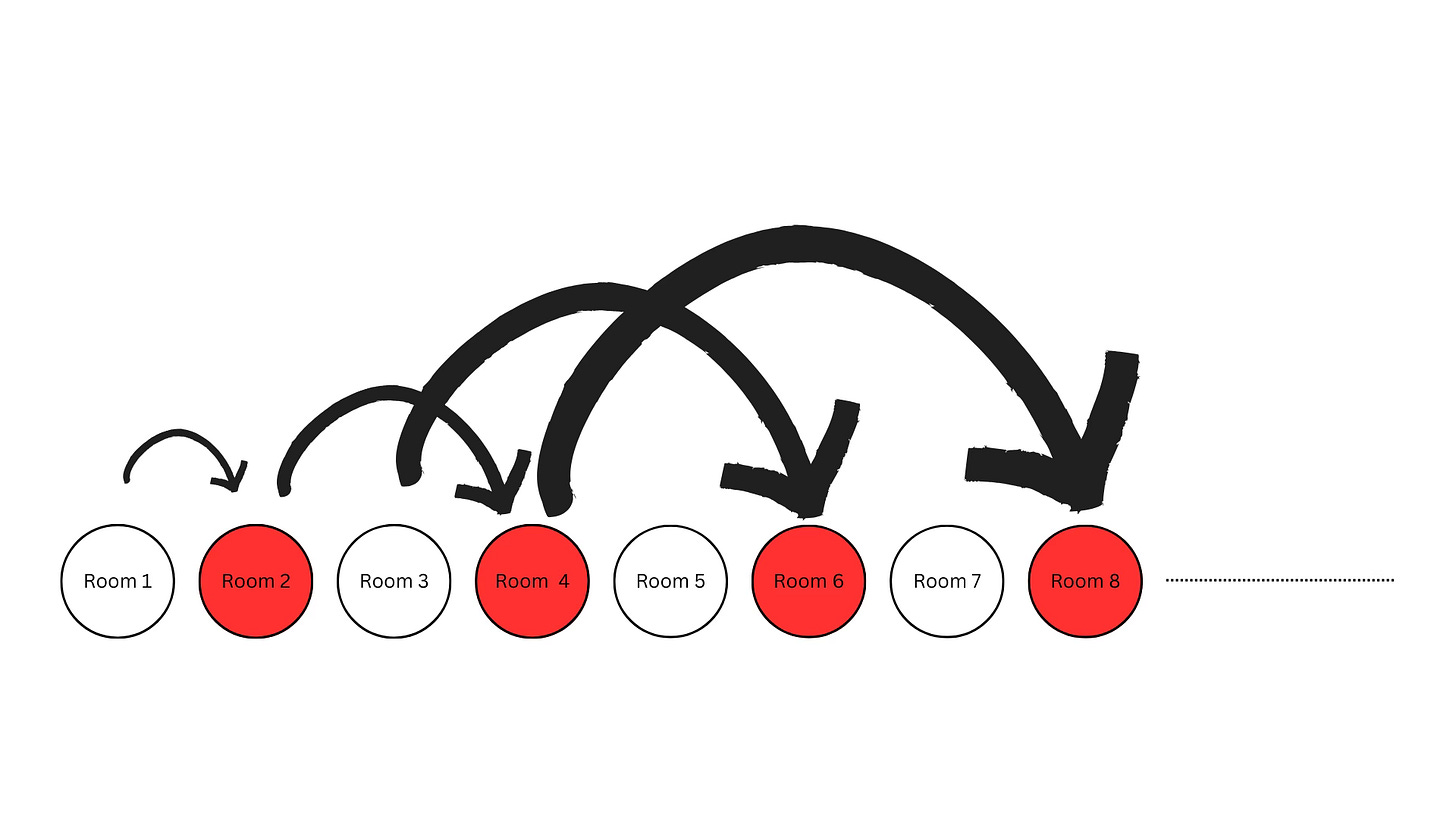
In general, whatever room you are in, move to double that room.

Again, everyone can do what you tell them to do: the person in room 1 moves to room 2, which is free because that person moved to room 4, which is free because that person moved to room 8, and so and and so forth.

But, at the same time, all the odd rooms just became free (see the Figure above).

So, you tell everyone in the infinite bus to stand in a line and send them to Room 1, Room 3, Room 5…There you have it: room for infinite people!

Let’s think again about what we have just done.

Your hotel had infinite rooms, but it also had infinite guests. Infinite people arrived, and you fit them all in! That is, you did something like:

\(\infty + \infty = \infty.\)

Infinite rooms can fit two infinite groups of people.

This is mind-blowing, but we can do even more.

Knock knock, knock knock, knock knock…
Knock knock, knock knock, knock knock…
Knock knock, knock knock, knock knock…
…

You see where I am going.

Imagine that now, infinite buses, each with infinite people, arrive to your door.

How do you fit them in?

If you can answer this, you have some really good ability for mathematics and infinity. You are trying to argue something like this:

\(\infty \cdot \infty = \infty.\)

Let me know your thoughts in the comments!

What’s coming:

• What to do with the infinite number of buses each with an infinite number of people.

• Is there something that the Infinite Hotel can’t fit? (Spoiler: there is!)

• Different sizes of infinity.

1. Yes, there are not infinite people in the world, but we are doing a mental experiment

2. These type of equalities don’t really make sense: the concept of adding that we are so used to doesn’t work with infinity. It is just an attempt of mine to encapsulate in an equation what we just did.