Why Big Numbers Reveal Big Truths: The Law of Large Numbers
How a Few Thousand Voices Can Speak for Millions
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Imagine this: it's election night, and pollsters declare a winner based on polling just 2,000 voters out of several million. Sounds impossible, right? Yet these predictions are close to the results with remarkable accuracy.
The secret isn't dark magic or crystal balls—it's one of statistics' most elegant principles at work. The Law of Large Numbers explains why small, carefully chosen samples can reveal profound truths about massive populations. It's the mathematical foundation that makes opinion polls, medical trials, and quality control possible.
Today, we'll explore this statistical wonder and discover why "going big" with numbers is our most reliable path to truth.
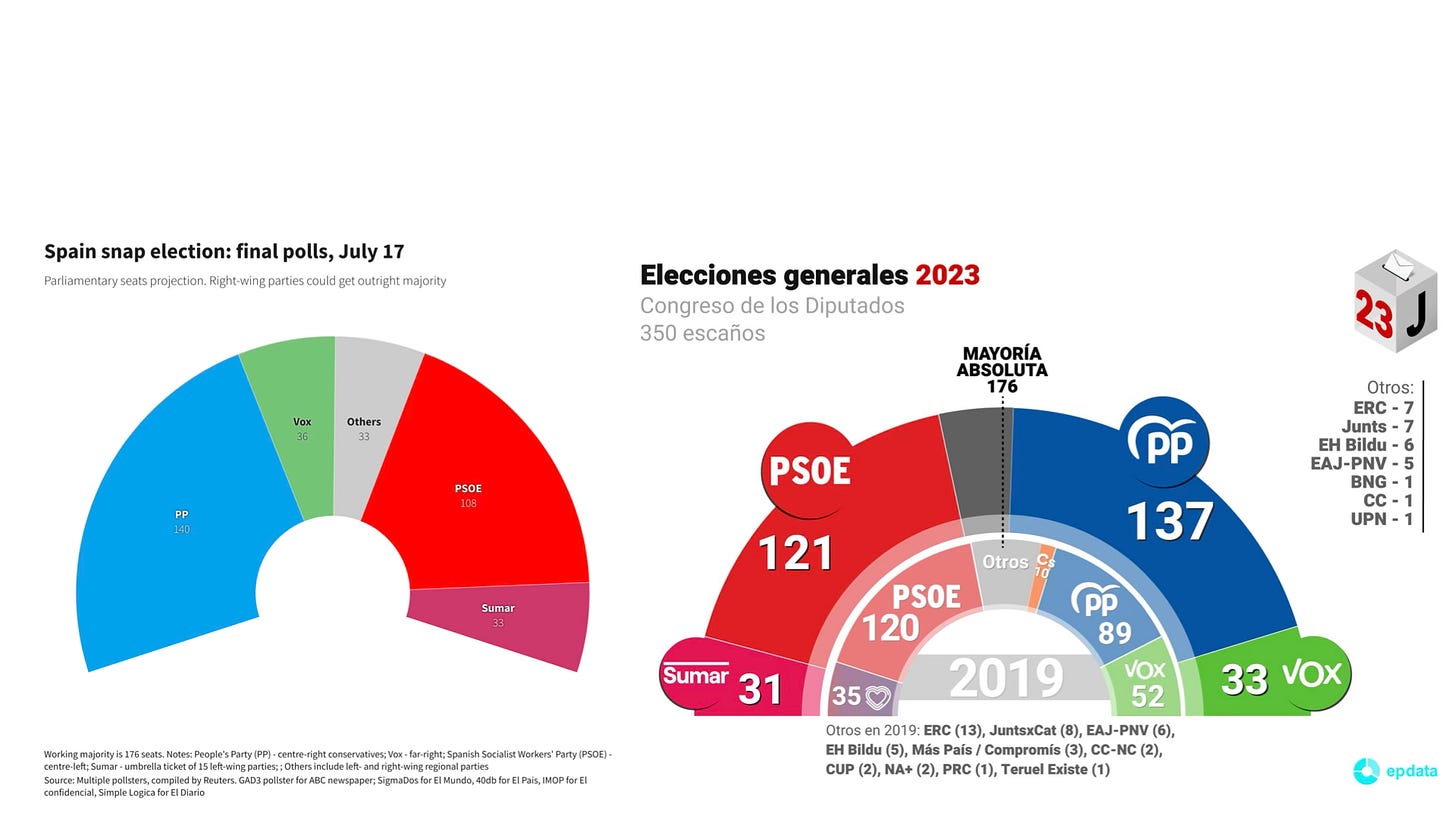
The Mystery: How Do Pollsters Do It?
Let’s start with a concrete example
Suppose you want to know what percentage of the population in Spain will vote for PSOE in the next election. That percentage exists as a fixed number somewhere out there—if we could magically ask every single Spanish voter, you could calculate it perfectly. The problem? You can’t feasibly ask 37 million people.
Instead, you do something that seems almost too good to be true: you ask a few thousand people, calculate their percentage, and declare that this represents the entire country.
This extrapolation from sample to population turns out to be not wild at all—it's precisely what the Law of Large Numbers guarantees will work.
The Law of Large Numbers: Your Statistical Superpower
Here's the formal definition, then we'll break it down:
The Law of Large Numbers
The average of a sample of independent, identically distributed random variables converges to the population average as the sample size increases.
Sounds intimidating? It's actually describing something really simple: poll enough people the right way, and you'll get remarkably close to the truth.
Let's unpack each part:
Random Variables: When Certainty Meets Chance
A random variable is just the name mathematicians use for "a quantity that varies randomly."
Here's the key insight: whether María specifically votes for PSOE isn't random—she knows her preference. But if I pick someone at random from Spain's population, their preference is random from my perspective. I genuinely don't know what I'll discover until I ask.
Independence: Why Your Friends Can Ruin Everything
Here's where things get tricky, and why many polls fail.
Imagine you're estimating the support for PSOE, so you poll someone and also their partner. Problem: couples often share political views. If María votes PSOE, Carlos probably does too.1
This creates "dependent" responses—they carry overlapping information rather than independent evidence. It's like asking the same person twice and pretending you got two opinions.
With strong dependence, the Law of Large Numbers can break down entirely. Positive correlations make your sample mean jump around more, requiring much larger samples to stabilize.
Identically Distributed: Comparing Apples to Apples
This is just a statistician’s way of saying that you should "make fair comparisons."
Want to know the average height of Spanish men? Sample Spanish men and measure their height—not Greek men, not Spanish women, and don’t measure their weight instead.
Most importantly, your sample must be representative: measure only people in Galicia, and you're measuring Galicia’s average height, not all of Spain's.
Convergence: Getting Arbitrarily Close to Truth
Remember when we learned that 0.9999… = 1? The sequence 0.9, 0.99, 0.999… gets as close to 1 as you want.
The same happens with polling averages. "Convergence" means:
Poll enough people, and you can get as close to the true answer as you want.
The LLN in Action: A Real Simulation
Let me show you the Law of Large Numbers in action with a real simulation.
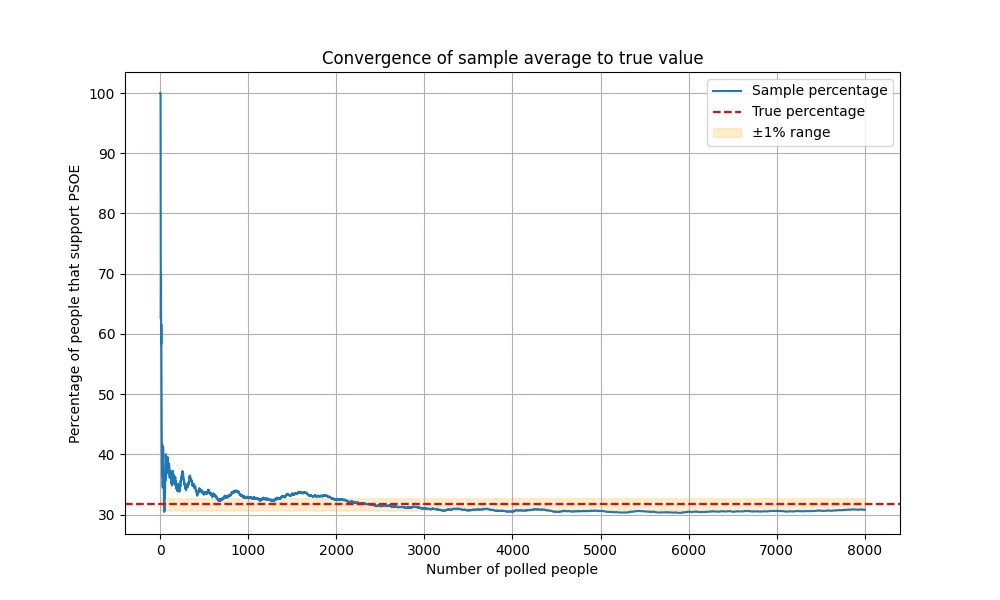
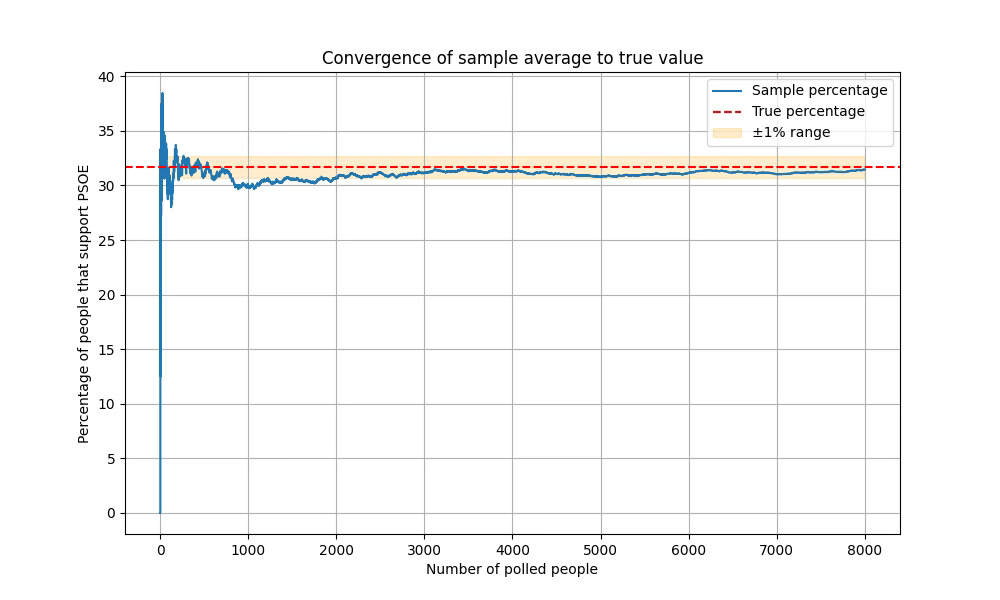
Imagine we somehow know that exactly 32% of Spain supports PSOE (roughly their 2023 election result). Now let's watch what happens as we poll 1, 2, 3… up to 8,000 random people:
As you can see in the figure, at the beginning our estimate is very poor.
After polling just one person (who happened not to support PSOE), our estimate is 0%—obviously terrible.
As we poll more (but still few) people, our estimate of the support for PSOE goes up and down erratically, reaching almost 40% in early stages and dropping below 30% with around 1,000 people polled.
The crucial thing is that, as the number of polled people increases, you can see how our estimate of the support for PSOE stabilises around the true value. This means two things:
It doesn’t vary much.
It stays close to the true value.
After about 2,000 people polled, the sample average stays within a 1% range of the real value of 32%.
If you run another poll with 8,000 new people, you will get a different graph, yet the phenomenon will be the same: as we poll more and more people, the sample average stabilises and approaches the true mean.
Why This Changes Everything
The Law of Large Numbers isn't just mathematical theory—it's the invisible foundation of our data-driven world.
It explains why pharmaceutical companies can test drugs on thousands of people and confidently predict effects on millions. Why manufacturers can inspect a few hundred products and guarantee quality across entire production runs. Why Netflix can recommend movies based on user patterns, and why your bank can assess credit risk.
The next time you ponder about the power of a poll, remember that mathematics guarantees that asking enough people reveals the collective truth.
In Case You Missed It
Remember: dependence doesn't mean couples always vote identically. It means that knowing María's choice changes the probability of Carlos's choice. María’s vote gives us information about Carlos’ likely preferences.