This is MathMadeSimple, by Álvaro Muñiz: a newsletter where you will discover how math appears in every aspect of your life, from decision-making to personal finance.
There is a sweet spot between risking too much and too little, and math can tell us precisely what it is.
When faced with a potentially profitable but risky bet, most people either wager too much or too little—both costing them money in the long run. The Kelly Criterion, developed by Bell Labs scientist John Kelly in 1956, solves this dilemma by calculating the exact optimal percentage of your bankroll to bet. This elegant mathematical formula is used by many, from professional gamblers to Wall Street titans like Warren Buffett and his partner Charlie Munger.
By mastering the Kelly Criterion, you can grow your wealth steadily while others around you either go broke from excessive risk or miss opportunities through excessive caution.
You have 100€ and will play 5 rounds of a dice game. In each round:
You win if the dice shows 1, 2, 3, or 4.
You lose if it shows 5 or 6
For each round, you can decide how much to bet.
If you win, you get your bet back plus the same amount (doubling your bet)
If you lose, your bet is gone
If you run out of money, game over.
For example, if you bet 50€ in the first round:
Rolling a 1-4 means you now have 150€ (100€ + 50€ win)
Rolling a 5-6 leaves you with just 50€ (100€ - 50€ lost)
How would you play in real life?
Real-Life Applications
This isn't just a hypothetical game. Similar decisions face us in real life.
Imagine you've discovered a promising startup. After careful research, you estimate it has a 10% chance of success. If it succeeds, you'll multiply your investment 20 times. With 5,000€ in savings, how much should you invest?
Should you go all-in for maximum potential return? Put in a small "safe" amount? Or is there a mathematically optimal answer?
The Expected Value Trap
One approach is to maximize your expected profit. If the game is profitable on average, this strategy tells you to invest everything.
This means that, on average, you'd double whatever you invest. Mathematically, investing your entire 5,000€ maximizes your expected profit.
But this is a terrible idea in real life! While you might make incredible money on average, what about all those times (90% of scenarios) when the startup fails and you lose everything?
Risk Aversion
This is where risk aversion comes in—the reality that most of us prefer certainty over uncertainty, even at the cost of potential profit.
Think about it: would you rather have a guaranteed 500€, or a 10% chance at 5,000€ (with 90% chance of 0€)? The expected value is identical, but most people choose the guaranteed money.
So when investing in our hypothetical startup, most people would commit only a fraction of their savings. This means a smaller potential win when things go well, but also means you won't be financially devastated when things go badly (which is most of the time with risky investments).
But what exact fraction of your money should you bet? Is there an optimal amount?
Loading...
Kelly Criterion
This is where the Kelly Criterion comes in—a mathematical formula that tells us the optimal betting amount.
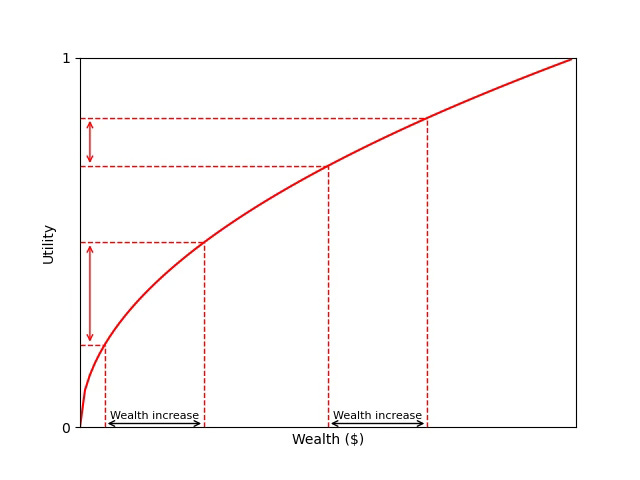
Instead of maximizing expected value, Kelly betting maximizes expected utility. Remember that utility is the actual value or satisfaction we get from money, and it looks something like this:
The key insight: the same amount of money provides diminishing utility as our wealth increases. Winning 100€ feels amazing when you have 50€ (tripling your money), but you barely feel it when you have 10,000€ (just a 1% increase).
The Kelly Criterion uses a logarithmic utility function1 (which mathematically captures our fear of losing everything) and gives us this formula:
KELLY CRITERION
For a bet where
p = probability of winning (e.g. p = 10%)
b = how many times your bet you win (e.g. if you bet 1€ and get 20€ back when winning, then b = 19).
The optimal fraction to bet is:
Kelly in Action
Let's apply Kelly to our dice game:
Probability of winning: p = 4/6 (or 2/3).
When you win, you double your bet, so b = 1
Then Kelly betting tells us we should bet 2/3 - (1 - 2/3)/1 = 2/3 - 1/3 = 1/3
This means you should bet exactly one-third of your money in each round. Not too aggressive, not too conservative—mathematically optimal.
For our startup example with a 10% chance of a 20x return, the Kelly fraction would be 0.1 - (1-0.1)/19 = 0.1 - 0.9/19 ≈ 0.053.
So you should invest about 5.3% of your savings, or around 265€ of your 5,000€.
What do you think? Is this how you would have acted in real life?
Visual Proof
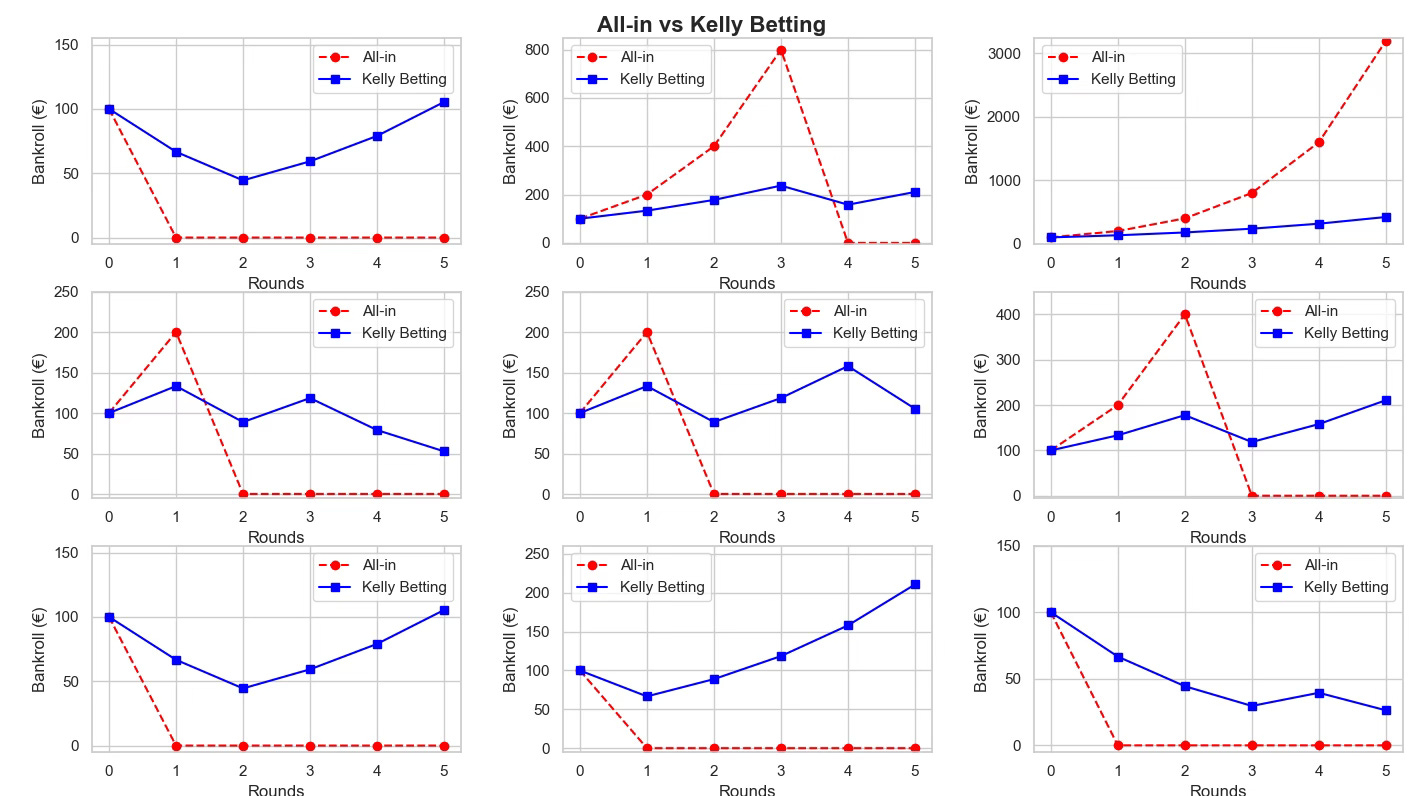
Here is what happens when you use Kelly betting:
The graph shows 9 different simulations of our dice game using two strategies:
Red lines: Going all-in each round
Blue lines: Using Kelly betting (1/3 of available money) each round
The results speak for themselves: Kelly betting ends up with more money in 8 out of 9 simulations. Why? Because the all-in player inevitably goes broke as soon as the dice shows a 5 or 6.
However, in the one simulation where a 5 or a 6 never showed, the all-in player made an astronomical 3,000€—far more than Kelly's modest 420€.
This perfectly illustrates the trade-off: the all-in strategy produces the highest average profit across all possible scenarios, but at the cost of going broke most of the time. Kelly betting won't make you as rich in the best-case scenario, but it protects you from ruin in all others.
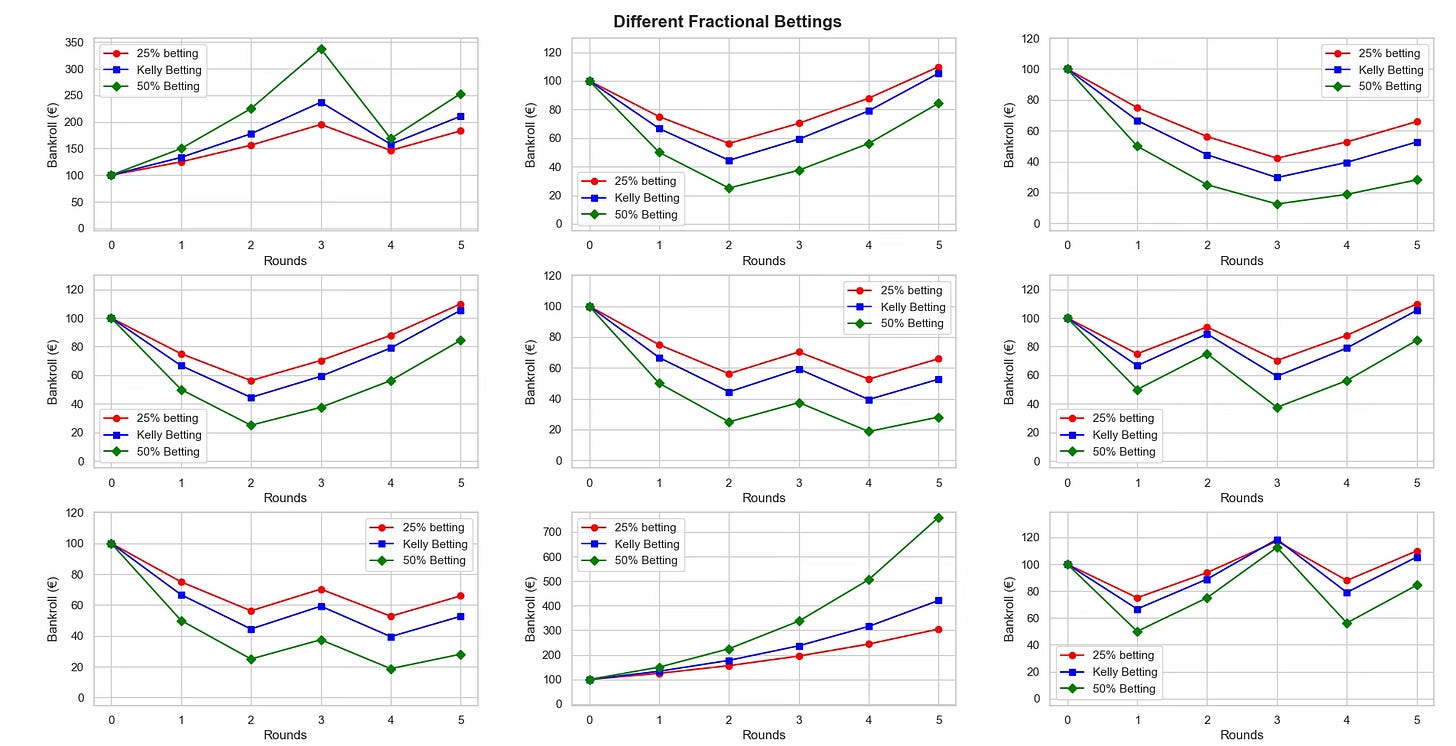
Lastly, here is a comparison of Kelly betting with other fractional bettings:
As you see, Kelly betting never makes the most money when things go well. But, when things go wrong, it is also never the biggest loser.
It finds the perfect balance between wins and losses.
Conclusion
Professional gamblers, successful investors, and poker champions use Kelly betting (or variations of it) to grow their wealth consistently over time. It's mathematical confirmation of the wisdom behind "slow and steady wins the race."
The next time you face a risky investment decision—whether it's stocks, crypto, sports betting, or that friend's startup idea—remember Kelly. Calculate your optimal bet size, and resist the temptation to go all-in, no matter how promising the opportunity seems.
As the old Wall Street wisdom goes: "Take care of the downside, and the upside will take care of itself."
More profit, more risk—nothing comes without cost.
Thank you for reading MathMadeSimple. If you enjoyed this post, please share with anyone that might enjoy it too
It looks very similar to the figure above, except that it approaches negative infinity as our wealth approaches zero. This implies that, when maximising log-utility, we will avoid going broke at all costs.
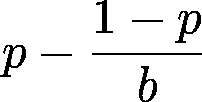
Loved it! It's cool to see how concepts we learnt in previous posts (like risk aversion) interact with the new information! 👏🏽👏🏽🥰