The Casino Always Wins: The Math Behind Roulette
From Naive Betting Strategies to Doob’s Optional Stopping Theorem
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
When I was a teenager, I spent some time wondering if I could come up with a clever strategy to beat the roulette—or at least make the game fair.
What if I placed a complex bet that somehow exploited the odds? Even if I couldn’t place a winning bet, could I create a sequence of bets that would guarantee a profit in the end? Fortunately, I only visited the roulette table a couple of times, lost quickly, and decided to quit.
Later, after studying math and probability, I found myself thinking, “What on earth was I doing?”
A Fair Roulette
Let’s put ourselves in a better position and consider a fair roulette.
A fair roulette has no 0. It consists of 18 red numbers and 18 black numbers.
In each round, you can bet on either red or black. Let’s say you bet 10€ on red:
If red comes up, you get back your 10€ and win 10€ more.
If black comes up, you lose your 10€.
In each round, your probability of winning is 50%. If you win, you double your bet; if you lose, you lose the entire amount.
Betting Strategies
Now, let’s look at some possible betting strategies.
A betting strategy is a predetermined method for placing bets in each round. Here are a few examples:
Strategy 1: In each round, I’ll bet 1€ on red.
Strategy 2: I will bet 1€ on red in Round 1, 2€ on red in Round 2, 3€ on red in Round 3, and so on.
Strategy 3: In each round, I’ll flip a coin and roll a die. If it lands on tails, I’ll bet the number shown on the die on red. If it lands on heads, I’ll bet the number on black.
…
How much money do you expect to make, on average, from each of these strategies? Here’s an important insight:
In any round, regardless of your strategy, you can expect to make 0€.
This is pretty obvious if you think about it. Remember that, at the end of the day, what we are doing is placing a bet on a game where we have a 50% probability to win, and where we either double our money or lose it all.
If you bet an amount X, half of the time you have a profit of X (you doubled your money), and the other half you have a loss of X (you lose your whole bet). On average, you get:
Stopping Times
here’s a subtlety in my earlier claim that "in any round, regardless of what you do, you expect to make 0€."
For example, consider the following strategy:
In each round, I will bet 1€ on red. As soon as I win, I stop playing.
How much do you expect to win in the final round?
By the way you have defined your strategy, the last round is always one in which you have won. Therefore, your expected profit in that round is 1€!
This looks promising. What if we go to the casino and do the following?
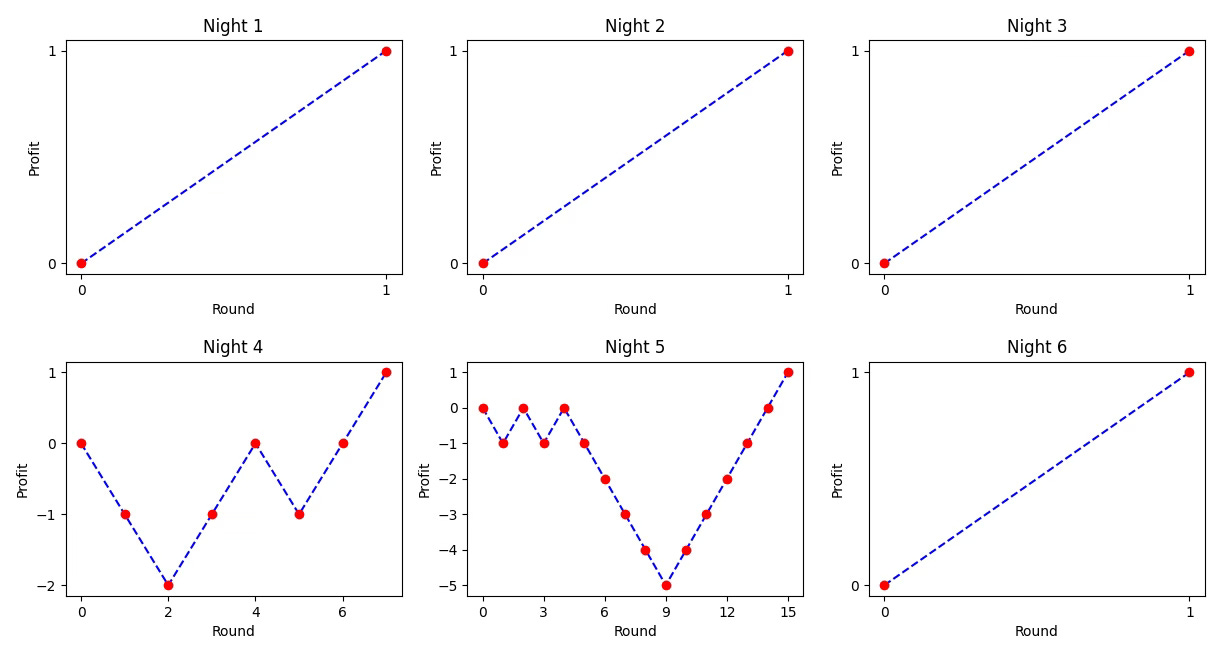
The Ultimate Strategy: on each round, I will bet 1€ on red. As soon as I have made some profit, I take it and leave the casino.
If you do this night after night, can you get rich?
For example, here are some simulations of what can happen on the first 6 nights:
By definition of your strategy, every single night you will leave the casino having made a profit (1€ of profit, but a profit). It is also possible to prove that the probability that your strategy takes infinite time (that is, that you never get to a point where you made a profit) is zero.
The Endless Wait
Have we truly found a strategy to beat the casino?
Before you go and try this, let me give you a spoiler: we have not.
The issue with the above strategy is subtle but crucial:
The probability that we never make a profit is zero. However, the expected number of rounds required to do so is infinite.
In other words, while this strategy will eventually end after a finite number of rounds with 100% certainty, the probability of reaching that end in a reasonable amount of time decreases so slowly that, on average, you’ll have to wait an infinite number of rounds.
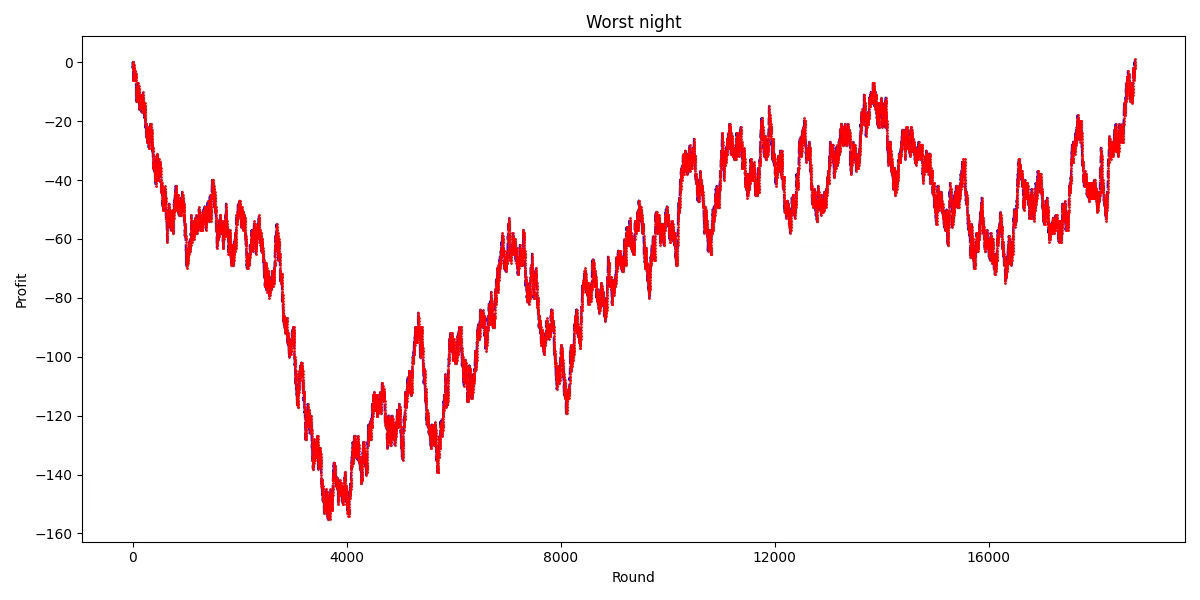
For instance, I have simulated 365 nights of playing this strategy (one for each night of the year). Look at what happens in the worst night:
Using this strategy for an entire year resulted in one night where it took almost 19,000 rounds to stop playing. In fact, for any arbitrarily large number of rounds, say 18,983,293, the probability of reaching that number is sufficiently high to make the expected number of rounds infinite.
Although you will always make a profit at some point, on average, you will wait forever!
Doob’s Optional Stopping Theorem
So, The Ultimate Strategy doesn’t work because, on average, you have to wait an infinite amount of time.
But what if we use a different strategy where we don’t have to wait forever? Is there still hope to make money at the casino?
Let me finish this post with this very nice mathematical theorem that I learned this past year:
Doob’s Optional Stopping Theorem (restricted version)
Any strategy where you stop playing after a specific condition is met—and that doesn’t require an infinite amount of time on average—will result in an expected profit of 0€.
I think this result is very cool. It is not saying "this strategy does not work" or "that strategy won’t work either"; it applies to any strategy you can come up with.
Essentially, Doob’s Optional Stopping Theorem is telling us that, it doesn’t matter how smart we are, there is no way we can come up with a strategy to win at the roulette.
If only I had known Doob’s theorem when I was a teenager!
In case you missed it
How You Can Make Better Choices (Spoiler: Self-Interest Fails)
Bitcoin 101: The Secret Power Behind Decentralized Electronic Money
From Profit to Utility: Approaching Risk in Financial Decisions



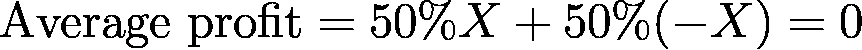
Now I'm 100% convinced to never go to a casino! Haha
Pues no lotería,.no casino. Habrá que seguir currando!