Selling your iPhone in 14 Days: How to Choose the Best Offer Using Math
How to Apply Probability and Expectation to Get the Best Deal in an Auction
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Imagine you want to sell your phone.
Each time you get an offer from someone, you have to tell them whether you accept the offer or not. If you decide not to, you can’t go back to that person. If you accept the offer, that’s the price you get for your phone.
How would you decide when to take an offer?
Today in a Nutshell
Today we learn how to approach situations where you need to decide whether to accept an offer or wait for a potentially better one.
These situations are very common in life: they appear when trying to choose a candidate in a sequence of interviews or when choosing a buyer for your home.
You will have a real game to play and try!
Auctioning
Imagine you want to sell something you own: this could be something like your old phone or even your house. Let’s stick with the phone example in what follows.
Every day, a potential buyer contacts you and offers you a price. You have to decide whether you take their offer or not.
If you decide not to, you can’t come back to it later.
If you take it, you don’t get to see the remaining offers.
Let’s assume for simplicity that each offer will be between $250 and $750, with each number in that range equally likely.
You need to have sold your phone in the next two weeks, so you will receive a maximum of 14 offers (one for each day).
How do you decide which offer to take?
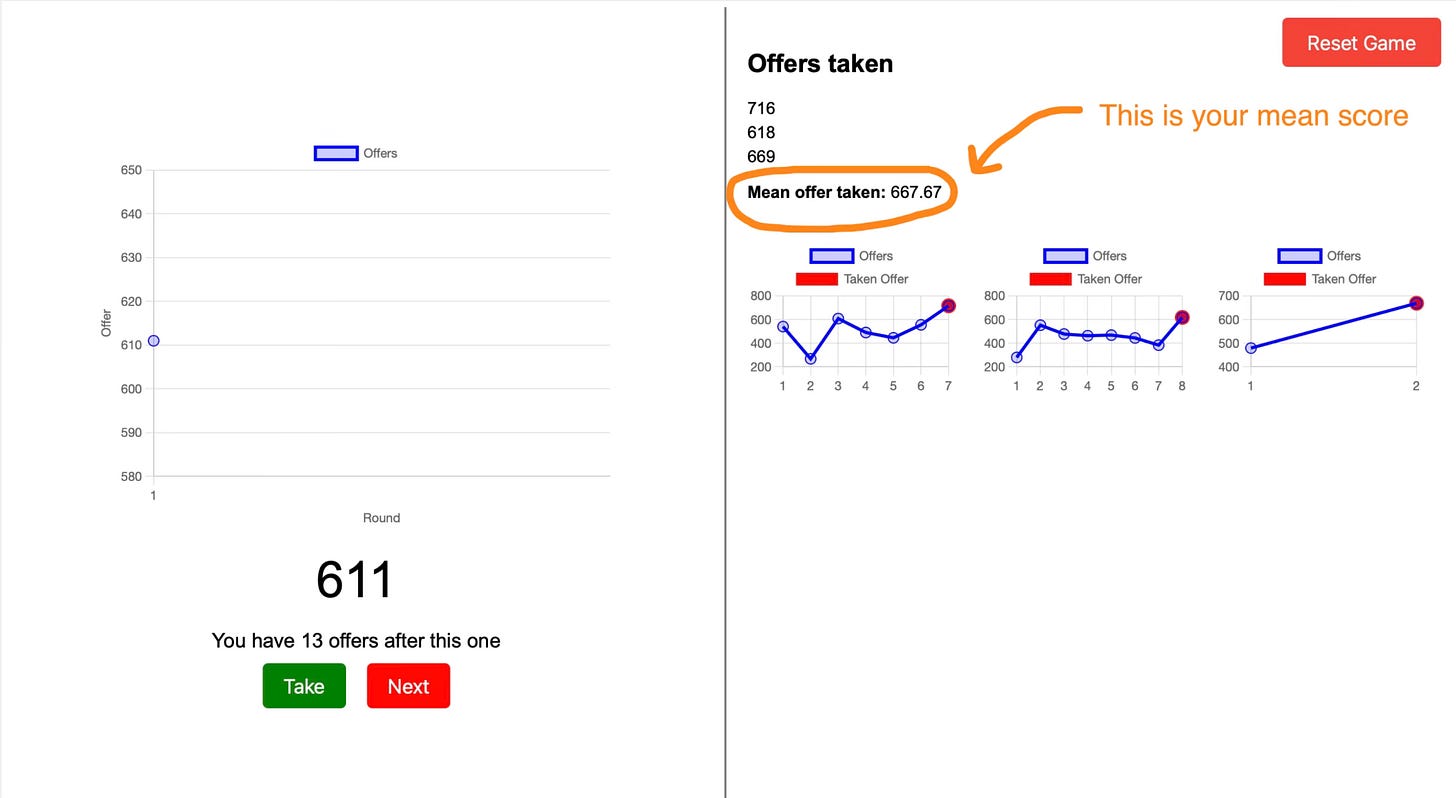
I have made a simulation of this game for you to try. Try playing with it and see what kind of deals you are able to make.
You can reset the game in the top right to start from zero and try new strategies. Once you are convinced with your strategy, play the game a bunch of times with that strategy and write down the average deal you got (see the figure below)—we will use this later.
PLAY THE GAME! (best on a computer)
How Did You Do?
What was your strategy when playing the game above? What was the average value you got for your phone?
Most likely, your strategy was something like ”If I get an offer above X, I will take it”.
It is intuitive, and it is a good starting point. But here is an important insight:
As rounds go by, you should lower your bar.
Surely you won’t take something like $500 in the first round: there are many rounds left, and you hope something better will come. But, as you approach the final round, you have less and less chances to get something higher.
Once again, mathematics can help us play optimally.
How to Get the Best Deal
To find the best strategy, we have to think of the two options we are given at each round:
We can either take the offer we are seeing, say $543.
We can wait for a future offer.
In the first case, we take $543 directly. In the second case, we don’t know what will happen: the offer that we will get in the next round (and the ones after) is random, it can be any number between $250 and $750.
As with any probabilistic game, where we cannot know with certainty what will happen, we need to work with expectations.
How much do I expect to win, on average, by waiting instead of taking the current offer?
Now here is the key. If you ask yourself the question above when you are at the first round of the game, it is very hard to figure out what you win on average by waiting. With so many rounds remaining, the range of possible outcomes makes it difficult to calculate the expected value of waiting.
Instead, we will use a trick that we have used in the past: we saw it when considering multiple rounds of the Prisoner’s Dilemma and when taking about risk with our betting game. We will start from the end:
If you are in the last round, on day 14, you have no choice: you will just take whatever you are offered.
Now imagine you are at day 13. You have two options:
Taking the offer you are given that day.
Waiting until the next day.
You don’t know what you will be offered the next day. But, on average, it will be $500. So here is what you do:
If on day 13 you are offered more than $500, you take that offer.
If on day 13 you are offered less than $500, you wait.
Now consider day 12. You have again two options:
Taking the offer you are given that day.
Waiting until the next day.
As before, we don’t know exactly what we will get if we wait. But we can think about what we will get on average. It is a bit trickier to calculate than before, but you can show that, by waiting, you will get $562.50 on average.1 So here is what we will do:
If we get offered more than $562.50, we take that offer.
If we get offered less than $562.50, we wait.
In general, starting from the end we can calculate iteratively what is the average profit we will obtain by waiting.
Here is what you get:

Given these values, we have the following strategy:
On any given day, if the offer we receive is higher than what we expect to win by waiting (‘minimum offer’ in the table above), we take that offer. Else, we wait.
Does This Work?
What was the average deal you got when playing the game before? If you haven’t already, go ahead and try your strategy for 5-10 games see what average score you get.
Let me show you what happens when you play with the optimal strategy we just developed:
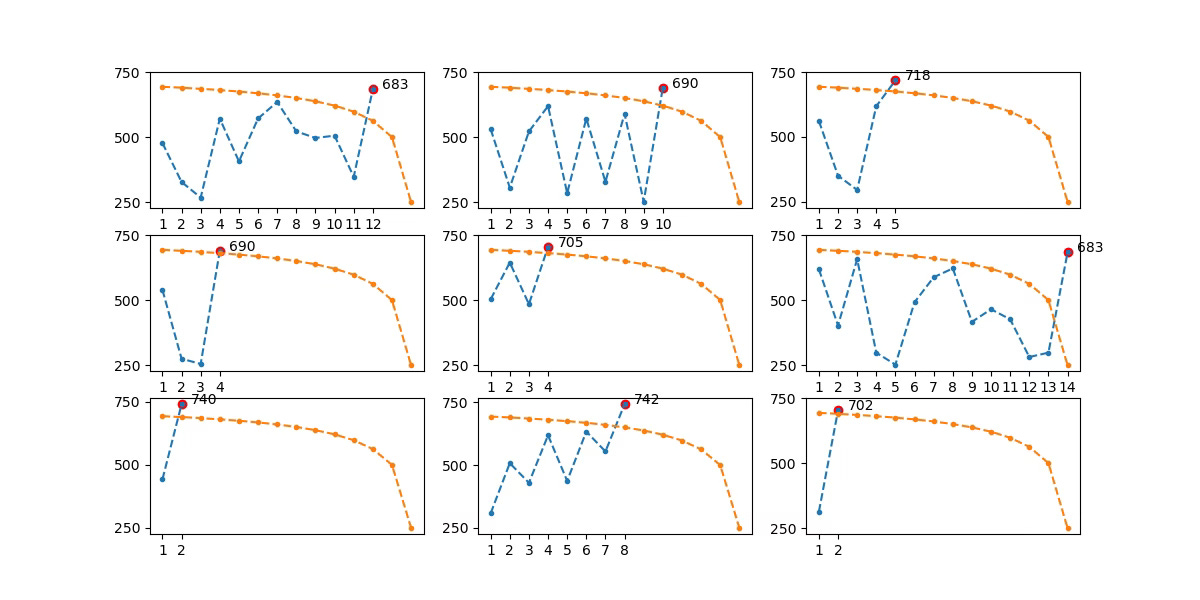
In orange I have shown the decision boundary: if at any point you get an offer that is higher than the orange line, you should take it. In blue I have shown several simulations of offers: when an offer crosses the orange line, we take that offer, marked in red.
Playing like this you will get, on average, a deal of around $696.
You can think of different strategies and try playing with them. If you play the game many times with that strategy (so that luck does not play a role), you will see you can’t do better than this!
A question for you:
We are making a crucial assumption to develop this strategy. Can you see what it is?
(Hint: we have talked about it before here and here.)
What’s coming:
How many rounds will we play, on average?
Kelly betting
Here is how you compute what is the average you will get by waiting on day 12.
On day 13, two things can happen:
Half of the time you will get an offer between $500 and $750, and you will take it. On average, this will be $625.
The other half of the time you will get an offer between $250 and $500, and you will wait and just take whatever you are offered on the last day. On average, you will be offered $500 on the last day.
So half of the time you get $625, and the other half you get $500. Your expected offer by waiting on day 12 is $562.50.


Maybe we're assuming the value of the phone stays the same through those 14 days?