From Profit to Utility: Approaching Risk in Financial Decisions

Understanding Why Humans Prioritize Security Over Potential Gains

This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.

---

The value you give to $100 depends on your current wealth.

When you are a kid and have nothing, getting $100 seems like a fortune to you. Get those same $100 as a pay raise when you are earning $50k and it will feel like there was barely no change. How much do you value money?

Today we will see that this question has a lot in common with how much you fear risk.

Today in a nutshell

• The utility of money is a measure of how much we value a certain amount of money.

• The utility you give to some amount of money depends on how much money you currently have: winning $100 is not the same if you have $1 than if you have $1,000.

• This way of valuing money forces us to fear risk!

The Utility of Money

In a previous post we saw that one of the properties of money is that it stores value. The value that money stores is an objective quality of money: you can do the same with $100 as Elon Musk can do with those $100.

Now, are those $100 worth the same for you and Musk? Certainly not.

Whereas $100 might be a considerable amount of money relative to what you have, those same $100 are a minutiae for someone like Musk.

How much we value money depends on how much we already have.

This is some subjective value we are assigning to money.

What you can do with a certain amount of money does not depend on how much money you already have. How much you value that money very much does.

Utility functions

To describe the way we value money we assign to it a utility.

This measures how much you value a certain amount of money. From the discussion above, our utility function looks something like this:

Possible utility function. For each wealth (x-axis), it assigns a utility (y-axis). The exact numbers are not important, but rather the shape of the function.

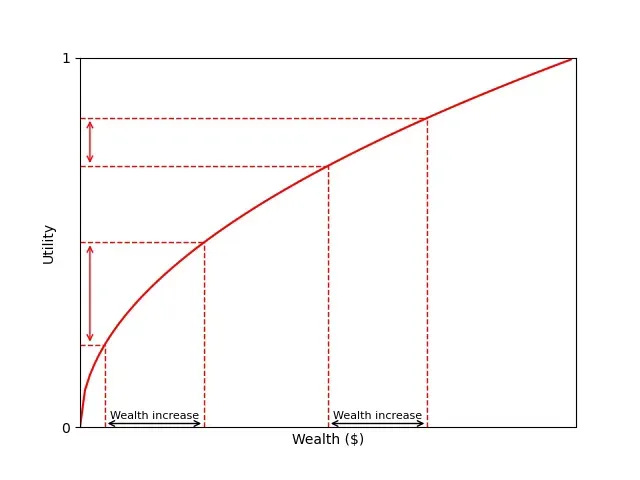
What is the key here?

I drew two increases in wealth of the same magnitude. One of them happens when you have little money (the one in the left), while the other happens when you have more money (the one in the right).

How does the utility (the value you assign to that new money) increase in each case?

We value increases in wealth less and less as our wealth increases.¹

That is, going from $10,000 to $20,000 is not the same to us as going from $50,000 to $60,000.

Risk Aversion

Last week we used a simple betting game to show how we humans fear risk.

If I give you the option to win $1,000 tomorrow no matter what or to flip a coin to either win $0 or $2,000, you would be crazy to take the second option. Both of them pay the same on average, but the second one has an uncertainty component. Why would you lose sometimes if you can always win?

Now consider instead the following two deals:

1. Tomorrow I give you $1,000, no matter what.

2. Tomorrow we flip a coin. It if lands on heads, you take $0. If it lands on tails, you take $4,000.

Now it is not clear whether you should take Option 1 or Option 2. While Option 1 has no uncertainty, it pays less on average: Option 1 pays $1,000 with certainty, but Option 2 pays $0 half of the time and $4,000 the other half, so $2,000 on average.

I asked a similar question in LinkedIn, and as you can see most people are also risk-averse.

If you had asked me a couple weeks ago which option I prefer, I would not have hesitated to say Option 2. I thought, as a rational mathematician, I should not get scared by the potential risk and just try to maximise my expected return.

If you ask me that today, I will say it is not a clear choice.

Why you Must Be Risk-Averse

Here is something that I recently learned and I think is pretty counterintuitive:

If you value money like we showed in the Figure above, you automatically fear risk.

I’ve always thought that the idea of valuing money less as you have more of it makes a lot of sense. For instance, we look at pay raises in terms of percentages, and we look at our expenses based on what our salary and savings are. This seems very intuitive.

On the other hand, I thought that risk-aversion was something ‘you could choose’. Some people can get more nervous with uncertainty, while others might be more tolerant and just trust in the long term.

I was wrong.

Any person that values money relative to what they have is inherently risk averse.

Let me give you a quick idea on why this is the case.

Concavity of the utility function

Equal pay-off

Let’s first analyse the simple case where we have equal profit, with and without certainty:

1. Tomorrow I give you $2,000, no matter what.

2. Tomorrow we flip a coin. If it lands on heads, you get $0. If it lands on tails, you get $4,000.

Why do we prefer Option 1, even though both have the same expected reward?

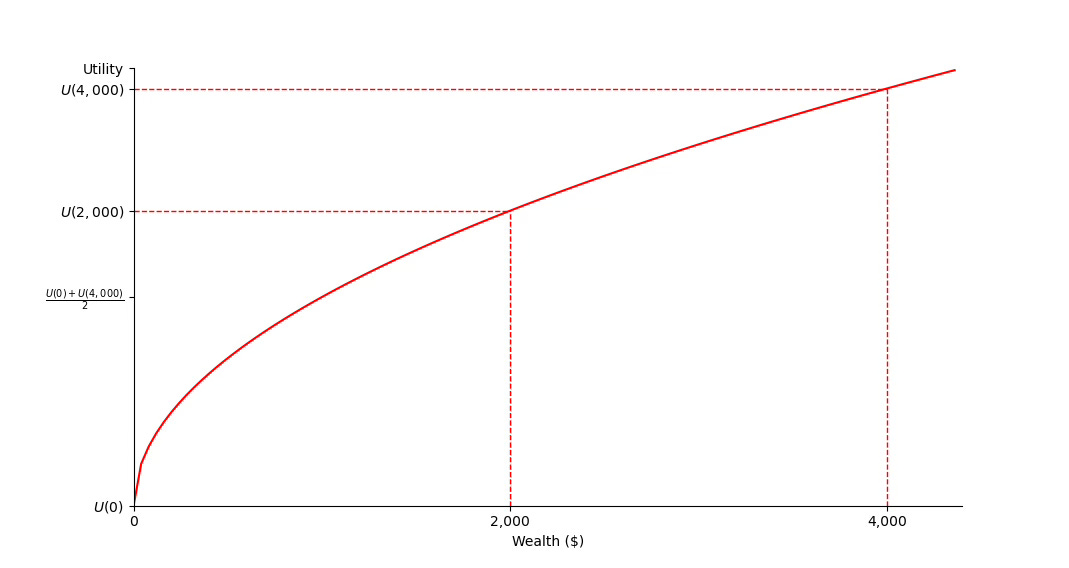
Instead of looking at dollars (money), let’s look at the value those dollars have for us (utility):

1. In the first case, you get $2,000 with certainty. So, the value of this offer to you is whatever utility you give to $2,000. Let’s call this U(2,000) (“utility of $2,000”).

2. In the second case, you get $0 half of the time and $4,000 the other half. So, the value of this offer to you is U(0) half of the time and U(4,000) the other half. So, the average value you give to this offer is [U(0) + U(4,000)] / 2 (the average of U(0) and U(4,000)).

The key here is the way the utility function bends. Look at the picture below:

You can see that [U(0) + U(4,000)] / 2 (the average of U(0) and U(4,000)) is less than U(2,000). In other words:

The average value we get from risking is less than the value of $2,000 with certainty.

This is the mathematical way of saying that we prefer certain outcomes to uncertain ones.²

Different pay-off

Let’s make things a bit more interesting and consider the case where risking has the potential of some extra profit:

1. Tomorrow I give you $1,000, no matter what.

2. Tomorrow we flip a coin. It if lands on heads, you take $0. If it lands on tails, you take $4,000.

The essential questions is:

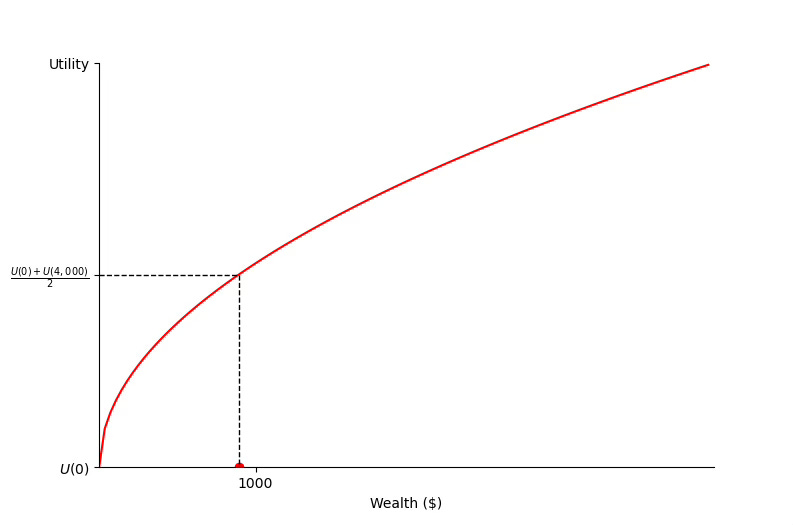
What is larger?

• U(1,000) (the value you give to $1,000 with certainty)

• [U(0) + U(4,000)] / 2 (the average value you get in Option 2)?

If you look at the Figure above and look at what wealth corresponds to [U(0) + U(4,000)] / 2, you will see in this case this is just below $1,000.

In other words, it is more valuable to you to take the $1,000 straight away instead of risking—even though you have the potential to win $4,000, and on average you win $2,000!

The specific numbers you get will depend on how much aversion you have to risk. People who tolerate risk better might find that flipping the coin has more value for them than the guaranteed $1,000. People who are very averse to risk might find that flipping the coin has even less value than in the figure.

The main point is that, regardless of how much risk averse you are, you will always value outcomes less the more uncertain they are (and, the more risk averse you are, the stronger this effect will be).

When risk is involved, you will ask for a corresponding extra profit.

Life and Risks

Here is a takeaway for you:

When taking a decision, you should not be greedy and just ‘aim for more profit’. Instead, you should aim for more value.

If life presents you with two alternatives, you should first estimate what is your expected value in each of them. Do not get lost in the profit—look at the value.

Crucially, this value varies from person to person, as it depends on:

• your current wealth;

• your risk tolerance.

Once you have your expected value for each option, choose the option that delivers the most value to you. You will find that, in many cases, the option that looked most profitable is not the most valuable.

Don’t risk unnecessarily just for the sake of increasing profit.

Be willing to risk when the increase in profit is large enough to deliver more value.

The fine line that divides both situations depends on the following:

How much do you fear risk?

What’s coming

• Why and how mathematical finance uses a reality where people are risk neutral

• What is the best strategy in last week’s game?

1. For the mathematicians in the room: the key is that the utility function, whatever its precise shape is, is concave.

2. More technically, the fact that the utility function is concave implies, due to Jensen’s inequality, that “the utility of the expected value is larger than the expected utility”.