Infinity and Beyond: How Some Infinities Are Bigger Than Others

How Mathematicians Compare Things That Never End

This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.

---

Infinity is a mind-blowing mathematical concept that challenges our everyday intuition.

Remember The Infinite Hotel thought experiment? It revealed some truly surprising results:

• The Infinite Hotel, even if completely full, can fit one more person.

• The Infinite Hotel, even if completely full, can fit infinite more people.

• The Infinite Hotel, even if completely full, can fit infinite groups of infinite people

Today we consider the following question: is there anything that The Infinite Hotel simply cannot fit?

How Mathematicians Measure Things

Comparing the size of two real-life hotels is straightforward.

If one hotel has 30 rooms and another has 200 rooms, one immediately knows that the second one is larger. Why? Because 200 is larger than 30? And why is this? Because 200 is 30 plus something else.

Why I am stating these obvious things? Because, once again, our intuitive "obvious" reasoning fails when dealing with infinity.

It is not necessarily true that infinite plus something is larger than infinity. Remember The Infinite Hotel: it can fit infinite people and be full, and also infinite people plus one more and still be full. The hotel hasn’t changed, so infinity is as big as infinity plus one.

What about infinite things?

We need a different way to compare the sizes of two infinite things.

Let me use the idea of a hotel size to introduce the relevant concept:

Comparing Hotels

We say that two (infinite) hotels have the same size if there is a way to match every room in one hotel with one room in the other, in such a way that all rooms are covered exactly once.

Let’s see some examples to understand this better:

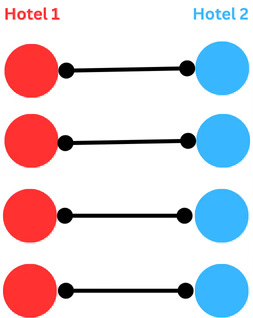
Example 1: Same Finite Size

Let’s take two hotels with 4 rooms each. They have the same size in the obvious sense, and also with our new definition—here is a pairing:

This is a valid matching to compare sizes, since:

1. Every room in Hotel A has an assigned room in Hotel B.

2. No two rooms in Hotel A are assigned the same room in Hotel B.

3. Every room in Hotel B has a match in Hotel A.

Example 2: Different Finite Sizes

Now let’s take two hotels, one with 4 and the other with 5 rooms. Here is what happens when you try to make a pairing between them:

The attempt in the left is not a valid pairing because the last room in Hotel 2 is not matched by any room in Hotel 1.

The attempt in the right is also not a valid pairing because the last two rooms in Hotel 1 are assigned the same room in Hotel 2.

No matter how hard you try, you won’t be able to come up with a valid pairing for these two hotels.

The Magic of Infinite Assignments

Now let’s look jump to infinity and see some more interesting matchings. For example, let’s see that a hotel with infinite rooms is as large as one with infinite rooms plus one extra room.

I’ll number the rooms of the first hotel by 1, 2 , 3… up to infinity. For the second hotel, let’s number its extra room as 0. The following pairing shows that these two hotels have the same size:

With this clever shifting of room numbers, we've created a perfect one-to-one matching. Therefore, these two hotels have the same size.

Similarly, being a bit ingenious, you can show that a hotel with infinite rooms has the same size as two hotels of infinite rooms combined. Even better, a hotel with infinite rooms has the same size as infinitely many hotels with infinite rooms combined!

What is Beyond Infinity?

We've developed a way to compare two infinite hotels. Now we are ready to answer our original question:

Is there anything that The Infinite Hotel cannot fit?

The Continuous Hotel

Imagine a hotel that has a room for every real number.

Real number is the fancy mathematical term referring to all numbers that we’re used to. These include the 'counting' numbers like 1, 2, 3 and so on, but also all decimals like 1.9837 and even weird numbers like π or √2.

Think about it: Between any two real numbers, there are infinitely many other real numbers. Between 0 and 1, you have 0.1, 0.01, 0.001, and infinitely many others. This density of numbers creates a different kind of infinity.

If you want the short story, here it is: The Continuous Hotel is larger than The Infinite Hotel.¹

If you want the long story, here is a famous argument in mathematics due to the German mathematician Goerg Cantor from 1874.

Cantor’s Diagonalisation Argument (Advanced)

Remember that two infinite hotels have the same size if there is a valid one-to-one matching between their rooms. In other words: two infinite hotels have different sizes if any matching between their rooms is not valid.

The word "any" is the key here. To show that two infinite hotels have different sizes, it’s not enough to show that this or that particular assignment doesn’t work: we need to show that any assignment will not work.

So let’s pick any assignment from The Infinite Hotel to The Continuous Hotel. For every room in The Infinite Hotel—which are numbered 1 to infinity—we have a matching in The Continuous Hotel. It will look something like this:

• Room 1 → Room 1.393849

• Room 2 → Room 78

• Room 3 → π

• Room 4 → 0.66666…

• …

Let’s show that, whatever this matching is, it will miss some room in The Continuous Hotel. I will use the above example to show you the idea, but note that this argument works for any matching:

• Room 1 gets matched to Room 1.393849. Let’s remember its first decimal digit: 3.

• Room 2 gets matched to Room 78. Let’s remember its second decimal digit: 0 (since 78 = 78.000…).

• Room 3 gets matched to Room π = 3,1416…. Let’s remember its third decimal digit: 1.

• Room 4 gets matched to Room 0.66666…. Let’s remember its fourth decimal digit: 6

• …

Now get all these digits and add 1 to them (if the digit was 9, we change it to 0). For example, in the example above we have the digits 3, 0, 1, 6 … and we change them to 4, 1, 2, 7…

Consider the number 0.4127… constructed this way.

This number has not been assigned to any room!

Why?

• It is not the number assigned to Room 1, since its first decimal digit (4) differs to the first decimal digit of the room assigned to Room 1 (3).

• It is not the number assigned to Room 2, since its second decimal digit (1) differs to that of the room assigned to Room 2 (0).

• And so on for every room.

Let’s recap what we’ve done:

1. We considered any arbitrary pairing from the rooms of The Infinite Hotel to the rooms of The Continuous Hotel.

2. We constructed a real number that cannot possibly be among those that the pairing covers.

3. Therefore, given any pairing from The Infinite Hotel to The Continuous Hotel, it misses some room!

Conclusion: The Infinite Hierarchy

What we've discovered is truly remarkable: not all infinities are created equal. The infinity of the real numbers (the "continuum") is demonstrably larger than the infinity of the counting numbers.

But the story doesn't end there. Mathematician Georg Cantor proved that there is an endless hierarchy of infinities, each larger than the last. He used a technique called the "power set operation" to show that for any infinity, you can always construct a larger one.

This leads to a dizzying sequence of increasingly vast infinities, labeled with the Hebrew letter ℵ (aleph):

• ℵ₀ (aleph-null): The size of the counting numbers (0, 1, 2, …)

• ℵ₁ (aleph-one): The next larger infinity

• And so on to infinitely many sizes of infinity

Even more mind-bending, mathematicians are still debating some fundamental questions about these infinities. The famous "Continuum Hypothesis" asks whether there is any infinity between the size of the counting numbers and the size of the real numbers—and amazingly, this question has been proven to be undecidable using standard mathematical axioms!

Infinity continues to challenge our intuition and stretch the boundaries of human understanding. As we've seen, when dealing with the infinite, the ordinary rules break down and we enter a realm where our everyday logic fails us. It's in this breakdown of intuition that we find some of mathematics' most profound and beautiful insights.

What other concepts might lie beyond our current understanding, waiting to revolutionize our thinking once again?

In Case You Missed it

• The Impossible Race: How a Tortoise Challenged Mathematics for 2,500 Years

• The Spanish Christmas Lottery: Dreams, Regrets, and the Reality of Your Odds

• The Limits of Democracy: What Arrow’s Impossibility Theorem Reveals about Fair Elections

• How You Can Make Better Choices (Spoiler: Self-Interest Fails)

What do you want next?

1. Be careful not to think “of course it is bigger! Real numbers include all counting numbers plus something else, so it is obvious there are more of them". Remember that this argument fails badly when dealing with infinity: there are as many numbers from 1 to infinity as there are from 100 to infinity, despite the first including the second plus something else!