How Holiday Planning Could Win You $1 Million
The Travelling Salesman Problem: From Galician Road Trips to the Deepest Unsolved Mystery in Mathematics
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Your next holidays could solve one of the greatest mysteries in mathematics.
Planning the perfect route through multiple cities seems simple enough—just find the shortest path and you're done. Yet this innocent travel dilemma connects directly to questions that have confused the world's best mathematicians for over half a century. The Clay Mathematics Institute considers it so important that they've placed a million-dollar bounty on anyone who can solve it.
What starts as holiday planning can become a journey into the fundamental limits of human knowledge.
How to Plan Your Holidays
You are planning your holidays to Galicia and you have a list of cities you want to visit: Santiago, A Coruña, Vigo, and Ourense.
You have to start and finish in Santiago, since that’s where you are flying to and from. To make the most out of your holidays, you ask yourself the following question:
What is the best route I can take to visit everything I want?
That is, should I go from Santiago to A Coruña, then to Vigo, then to Ourense and back to Santiago? Or should I go from Santiago to A Coruña but visit Ourense before Vigo? What about going to Vigo first instead of A Coruña?
Fortunately, for your four-city holiday itinerary, it’s quite easy to solve—you can play with Google Maps to find the fastest route.
Algorithms—The Backbone of Computers
The problem above is very common in real-life.
It appears when you plan your holidays, when Amazon decides in which order to deliver their packages, or when you’re running errands and want to optimise your order.
What we just did was follow an algorithm to solve this problem:
List out all possible routes you can take.
For each route, input it into Google Maps and note the total time.
Choose the route with the minimum total time.
An algorithm is a set of rules such that, given any input, they can be followed unambiguously step by step to arrive at a solution to a problem.
If I give you any list of cities, you can run this algorithm and find the best solution.
So, why am I talking about something so simple?
When Simple Becomes Impossible
In the example above we had 3 intermediate cities we wanted to visit: A Coruña, Vigo, and Ourense. There are only 6 possible routes we could take:
Santiago—A Coruña—Vigo—Ourense—Santiago
Santiago—A Coruña—Ourense—Vigo—Santiago
Santiago—Ourense—A Coruña—Vigo—Santiago
Santiago—Ourense—Vigo—A Coruña—Santiago
Santiago—Vigo—Ourense—A Coruña—Santiago
Santiago—Vigo—A Coruña—Ourense—Santiago
You can just try all 6 combinations in Google Maps and find out which is the best route (see the figure above).
Now imagine that instead of 3 intermediate stops you have 4. How many possible orders can you have?
Here's how the math works:
You first choose which will be your first stop. There are 4 possible choices for this.
After this choice, you need to choose your second stop. There are 3 possible choices for this (since you already chose your first stop).
You then choose your third stop, for which you have 2 choices remaining.
Finally, the last city you visit is the remaining one.
In total, there are 4 x 3 x 2 x 1 = 24 possible routes you can take.
The numbers explode quickly:
For 5 intermediate stops: 120 routes
For 6 intermediate stops: 720 routes
For 10 stops: 3.6 million routes
For 20 stops: 2.4 quintillion routes (that's 18 zeros!)
For an Amazon driver who might be stopping at 100 different places on a given day, there are so many possible routes that even if all atoms in the universe were computers, and they tried to solve the problem since the Big Bang, they wouldn’t have finished!
The possibilities grow really fast with the number of stops.
This explosion makes the approach described above—listing out all possible routes, computing the time for each, and choosing the fastest one—completely infeasible in real life. Although it works in theory, it doesn't in practice.
P vs NP—The Biggest Problem in Computing
What we've been describing has a name: the Travelling Salesman Problem (TSP).
Imagine a salesman who needs to visit a number of cities exactly once and return to his starting point, while minimizing the total distance traveled. Sounds familiar? That's exactly what we did with our Galician holiday!
The TSP is one of the most important problems in mathematics and computer science.
Above we described an algorithm that works, but it’s very slow. For 4 cities, it needs to check 4 x 3 x 2 x 1 combinations. For 7 cities, this number jumps to 7 x 6 x 5 x 4 x 3 x 2 x 1. In general, for n cities, it needs to check n x (n - 1) x (n - 2) x … x 2 x 1 combinations.
In mathematics, given some natural number n (e.g., 7), the factorial of n, written as n!, is equal to n x (n -1) x … x 2 x 1 (e.g., 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1).
Our algorithm "runs in factorial time". This is just a fancy way of saying that, for n intermediate cities, it needs something like n! operations to solve the problem.
Computer scientists consider an algorithm to be "fast" if it runs in polynomial time: for n intermediate stops, it needs n, n^3 or n^20 operations to solve the problem.
Polynomial growth is much slower than factorial growth:
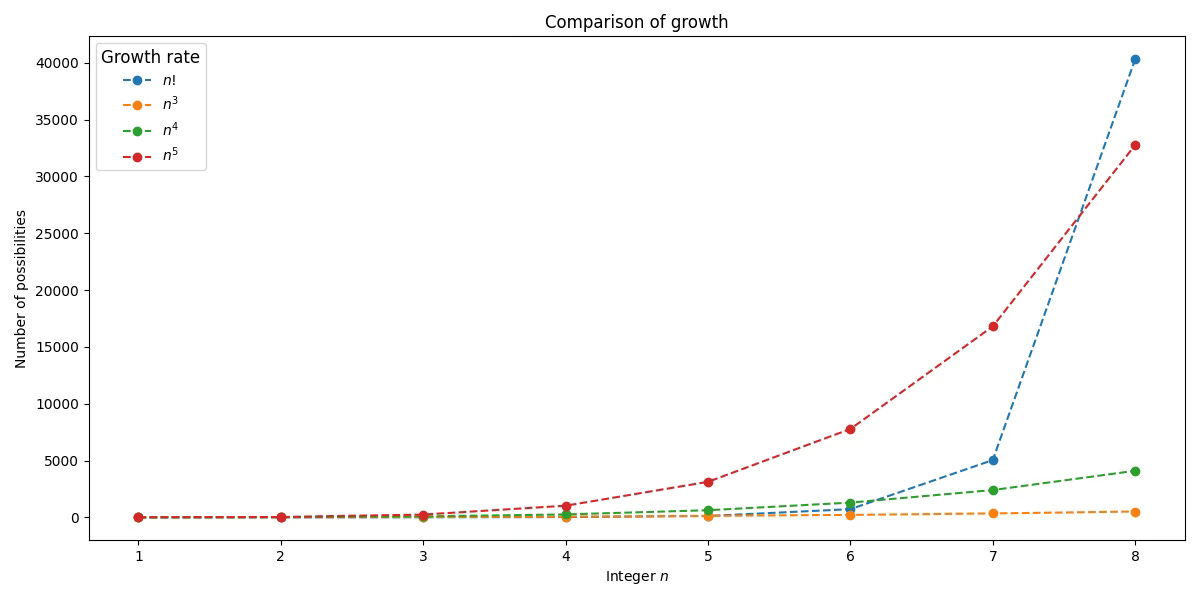
In other words, any polynomial growth is vastly better than factorial growth.
Here’s the kicker:
Up to this day, we don’t know of any algorithm that solves the TSP in polynomial time.
And here’s something mind-blowing:
If you found an algorithm that solved this problem in polynomial time, you would win one million dollars.
The Million-Dollar Question
In 2000, the Clay Mathematics Institute published a list of seven very important problems in mathematics, which they called the Millennium Problems. Each comes with a $1 million prize for whoever solves it.
Among them is the so-called P versus NP problem, which asks something like the following:
If I can verify whether a solution of a problem is right or wrong in polynomial time, can I also solve the problem in polynomial time?
Problems for which I can verify whether a solution is right or wrong in polynomial time are called NP problems, and problems that I can solve in polynomial time are called P problems. The P versus NP problem asks whether these two classes are the same.
The TSP (with a slight modification) turns out to be an NP-complete problem: if you can solve it in polynomial time, you can solve any other NP problem in polynomial time. Thus, if you found an algorithm to solve the TSP that runs in polynomial time, you could solve any other NP problem in polynomial time, showing that P = NP.
Why This Matters Beyond Holiday Planning
The implications go far beyond vacation planning.
Efficient solutions to the TSP would revolutionize:
Logistics and delivery: Companies like Amazon, UPS, and FedEx could optimize millions of delivery routes.
Manufacturing: Circuit board drilling, robotic assembly lines, and supply chain optimization.
Biology: DNA sequencing and protein folding analysis.
Cryptography: Many of our security systems rely on problems being hard to solve but easy to verify.
The P vs NP question isn't just a curiosity—it's about understanding the fundamental limits of computation itself.
If P = NP (meaning every problem that's easy to verify is also easy to solve), it would transform virtually every field that relies on computation.
If P ≠ NP, it would confirm that some problems are inherently difficult, no matter how clever our algorithms become.
So the next time you're planning a road trip and trying to figure out the best route, remember that you're dealing with one of the deepest unsolved problems in all of mathematics.
And who knows? Maybe your insights over morning coffee could be worth a million dollars…




Now it makes sense that holliday planning takes so long 😂😅