The Birthday Problem–Should You Take My 100€ Bet?
The Counterintuitive Math that Will Change How You See Coincidences
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Your brain is a terrible probability calculator.
What feels obviously true about randomness and coincidence is often wrong, leading us to make poor decisions in everything from gambling to cybersecurity. Mathematicians have known this for decades—the gap between human intuition and mathematical reality creates some of the most shocking discoveries in probability theory. Even the smartest people consistently fail at estimating the likelihood of seemingly rare events, costing them money, opportunities, and credibility.
Today's simple birthday question will prove just how unreliable your instincts really are.
The Birthday Problem
Imagine tonight Barça and Madrid clash in El Clásico.
Picture this: 22 players sprint across the field (11 per team), plus one referee keeping order. That's 23 people total. Now, here's a bet that I offer you:
If any two people on that field share the same birthday, I'll give you €100. If not, you give me €100.
When Math Beats Intuition
If I offered you €100 for heads on a coin flip but asked for €100 on tails, you'd know it's a fair deal—50/50 odds.
Instead, I am offering you a deal where you win 100€ if there is a common birthday, and you lose 100€ if not. Therefore, the question you should ask yourself is:
Is it more likely that there is a common birthday, or that there isn’t?
More specifically:
What is the probability that there is a common birthday?
Your intuition probably says birthdays are spread out randomly, so finding a match among just 23 people seems unlikely. Is it really?
Probability—a powerful branch of mathematics—helps us make optimal decisions when facing uncertainty.
The Hard Way vs. The Smart Way
Assuming we don’t know the birthdays of any of the players or the referee, how can we tackle this problem?
The Hard Way
For two people to have the same birthday, we could calculate the probability of every possible scenario:
There are exactly 2 people among the 23 with the same birthday (that is, among the rest of the people none of them share the same birthday).
There are exactly 3 people with the same birthday.
There are exactly 4 players with the same birthday.
And so on and so forth, until the (pretty much impossible) case that everyone has the same birthday!
We could try to compute the probability of all of the scenarios above, and then add all of them together. However, these are a lot of cases to consider!
Can we do any better?
The Smart Way: Your Favourite Probability Trick
I’m going to tell you one of the most useful tricks to deal with probability computations that seem to have too many cases.
It’s based on the following simple observation:
Exactly one of the following things must be true:
At least two people share a birthday.
No one shares a birthday.
Since one of the two things above must happen, their probabilities add up to 1 (or 100%).
If we can find the probability that no one shares a birthday, we can subtract from 1 to get our answer. This turns a complex problem into a manageable one.
The Calculation
(Feel free to skip this section if you prefer the bottom line!)
Imagine an unmarked calendar with all 365 days available.
Person 1: Can be born on any day. Probability of no conflict = 365/365 = 1.
Person 2: Can be born on any of the remaining 364 days. Probability = 364/365.
Person 3: Can be born on any of the remaining 363 days. Probability = 363/365.
Person 4: 362/365.
...and so on for all 23 people.
The probability that NO ONE shares a birthday is:
The Shocking Answer
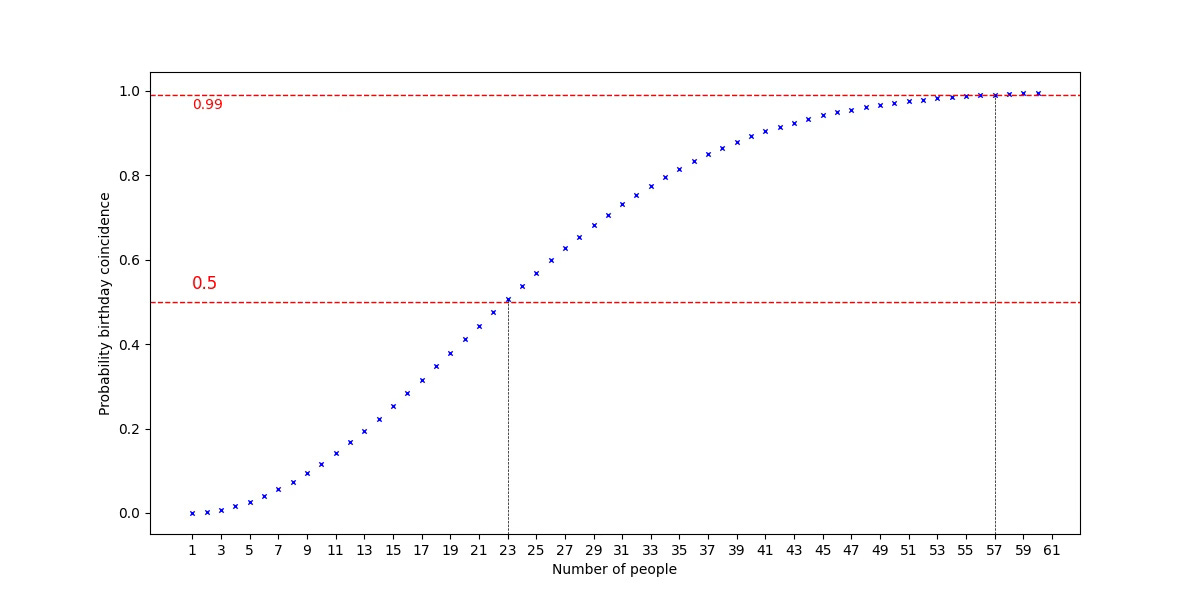
The probability that at least two people share a birthday is approximately 51%!
You should absolutely take my bet—you're slightly more likely to win than lose.
Even more surprising: 23 is the magic number where the odds tip in your favor. With 22 people (no referee), the probability drops just below 50%, making the bet unfavorable.
The numbers get dramatic quickly:
30 people: 70% chance of a match.
50 people: 97% chance.
57+ people: >99% chance.
Why Our Intuition Fails Us
The secret lies in pairs.
Among 23 people, there aren't just 23 potential birthdays to consider—there are 253 possible pairs of people who could share a birthday:
Person 1 could match with any of 22 others.
Person 2 could match with any of the remaining 21 (we already counted Person 1 matching Person 2 above).
Person 3 with any of the remaining 20.
...and so on.
With 57 people, you get 1,596 possible pairs!
Each pair represents another chance for a birthday match, which is why the probability climbs so rapidly.
Beyond the Football Field
This principle appears everywhere:
Cybersecurity: the birthday paradox limits how secure hash functions are against collisions, enabling “birthday attacks” that exploit this math to find duplicates faster than brute force.
DNA evidence: the birthday problem helps assess the chance of accidental matches within large DNA databases, critical for understanding false positive risks and non-uniqueness of DNA profiles.
Social networks: the birthday problem explains why in relatively small groups you often find mutual friends or shared connections, reflecting how quickly overlaps appear in large networks
The Takeaway
Next time someone offers you a birthday bet with 23+ people, remember: mathematics beats intuition. The birthday problem reveals how our brains struggle with probability and combinatorial questions.
So, would you take my €100 bet now?
What other counterintuitive probability problems fascinate you? Reply and let me know what you'd like to explore next!


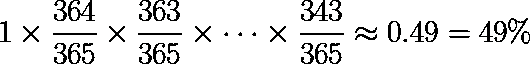


Está claro que en este caso la intuición falla, pero ¿es importante la intuición en las matemáticas?
Apparently it's very easy for me to get scammed 🙃hahha