Public Key Cryptography: How Math Secures the Internet
From WWII Codebreaking to Quantum-Proof Security
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Every time you shop online, check your bank account, or send a private message, you're trusting your most private information to a mathematical idea from the 1970s.
This system, called public key cryptography, solved what back then seemed like an impossible puzzle: how to send secrets to someone you've never met, across networks filled with potential malicious intermediaries, without ever sharing a password beforehand. Before this innovation, secure communication required meeting in person or trusting couriers—imagine if every online purchase required you to fly to the company's headquarters to exchange secret codes. The mathematics behind this system are so elegant that it turned the entire concept of secrecy on its head, making the "lock" public while keeping only the "key" private.
Today, this breakthrough protects trillions of dollars in transactions and billions of private conversations every single day.
The Old Way
Let’s start with the way things were done before the mid-1970s.
For instance, this is the type of cryptography used by the Nazis during WWII with their famous Enigma machine.
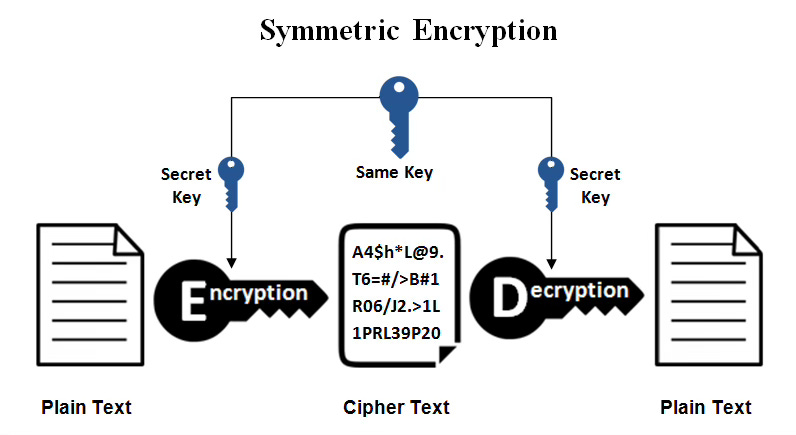
Goal: Get a message from a sender to a receiver in such a way that, if intercepted by an unauthorized person in the middle, the unauthorized person can’t understand it.
Idea: Encryption/decryption procedure.
The sender encrypts the message, making it inaccessible for any unauthorized party. Let’s think of this as putting the message into a box and locking it with a key.
The receiver decrypts the message, making it readable again. With the same analogy as before, we think of this as opening the box and pulling out the message inside.
Now here is the key difficulty in implementing this:
The sender and the receiver must both have the key that encrypts/decrypts the message (the key that opens/closes the box).
How do we generate the keys in a secure way?
Let’s say the sender is the one generating the keys (i.e., creating the lock and its keys for the box). Then, how does he send the key to the receiver?
We are back at the start! We have a private thing we want to send to a receiver (the key), and we need to do it in a secure way. If we apply the same idea again, we will end up with keys within boxes within boxes within boxes…
Instead, the only way would be to either meet in person to exchange the keys, or have a trusted courier to deliver the key to the receiver. Possible, but very expensive if you want to exchange a lot of messages.
Imagine if every time you wanted to buy something on Amazon, you had to first fly to Seattle to secretly exchange passwords with their security team!
The Great Insight: Public-Key Cryptography
In 1970, British cryptographer James Ellis had an idea so revolutionary it seemed impossible: what if you could send someone a lock, but keep the key?
The idea was the following:
Public Key Cryptography
The receiver keeps secret to himself a secret key (also known as private key). This key can decrypt the message. (In our analogy, the receiver creates a special lock and keeps the only key that can open it.)
The receiver also generates a public key. This is a key that can encrypt the message. (Think about it as a mechanism that can close the lock, but not open it.)
Since the public key can only encrypt messages, and not decrypt them, there is no need to keep it private. It's like giving away copies of a device that can close your mailbox, but only you have the key to open it and read what's inside.
Think of it like this: you create a special mailbox and put it on a busy street corner. Anyone can drop a letter in (encrypt), but only you have the key to open it and read the contents (decrypt).
One-Way Functions
This idea, as clever as it is, has an essential problem.
The receiver creates a lock and the key to open it (their secret key). Associated with this lock and key, he creates the public key with which senders can encrypt messages for him. The question is:
How can we make sure that, given the public key, it is impossible to recover the private key?
In other words: we need a way to produce a public key from a private key, in such a way that we cannot recover the private key from the public key.
This is what mathematicians call a one-way function: given any input (private key), it produces an output (public key), but it is extremely hard to take an output (public key) and figure out which input (private key) it came from.
Although Ellis himself did not figure out how to do this, his colleague Clifford Cocks implemented such a method a couple of years later.1
RSA—The Cornerstone of Internet Security
The encryption method that Ellis and Cocks came up with underlies most of today’s Internet security.
It is called the RSA cryptosystem, since it was publicly described by R. Rivest, A. Shamir, and L. Adleman in 1977 (Ellis and Cocks’ system was kept classified by the UK government).
The mathematics that underlie the encryption and decryption process, as well as the justification for why they are secure, are unfortunately well beyond the scope of this newsletter (you can watch around min. 10 of Cocks’ talk or check out Wikipedia if you are interested).
However, the way that public and secret key pairs are generated is surprisingly quite simple.
Suppose you are the receiver. You want to generate:
A private key: something that only you know.
A public key: something related to your private key that everyone can know.
These should have the property that, given the public key, it is extremely hard to find out the private key.
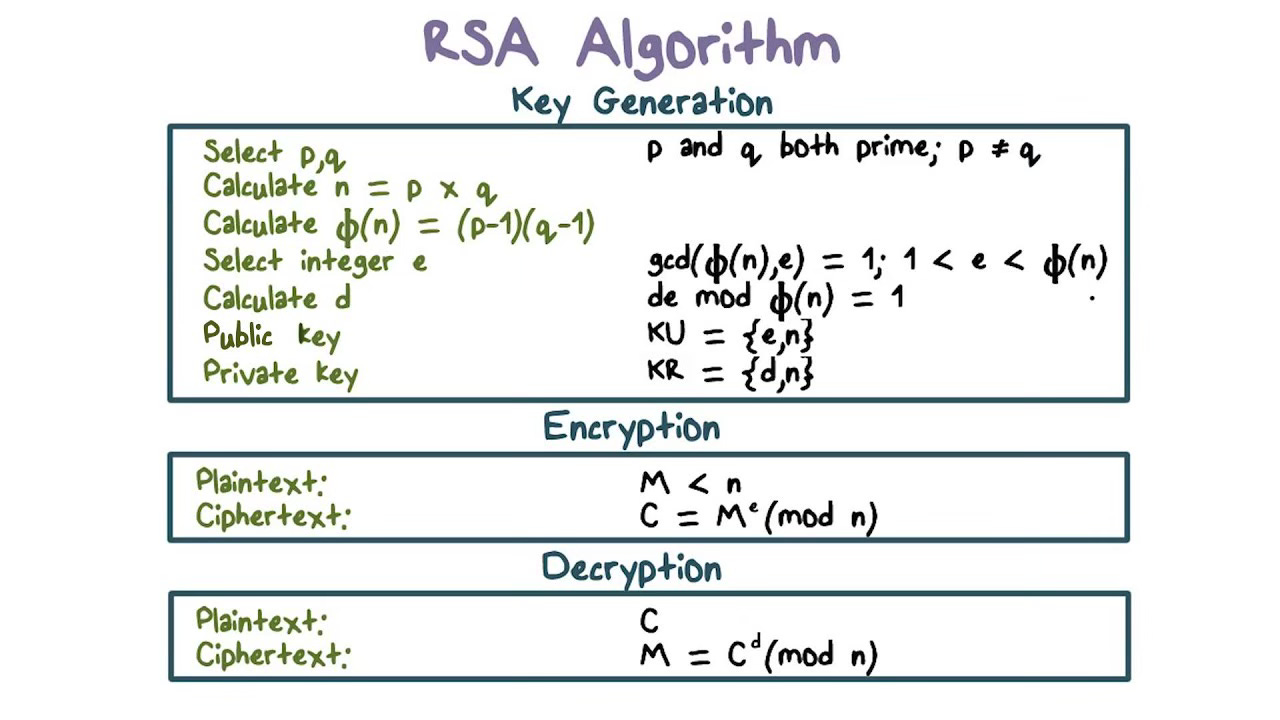
The RSA cryptosystem uses prime numbers: numbers that can only be divided by themselves and 1—like 2, 3, 5, 7 or 11, but not 4 (it can be divided by 2). It works as follows:
The private key will be a very large prime number p, say 7,879.
To generate the public key, we first choose another very large prime number, say 6947. The public key will then be the product N = p x q = 7,879 x 6,947 = 54,735,413.
Now here is the crucial thing:
Given a very large number like 54,735,413, there is often no better way to find its factors than pure guessing.
That is, if I only give you 54,735,413 (the public key), to find a number that divides it (that is, 7879, the private key), you have to try, one by one, all the numbers from 1 up to 54,735,413.
Technically you can do it, but for truly 'very large' numbers (see below), you will die before you guess it!
Very Large Really Means Very Large
The primes I chose, 7,879 and 6,947, are by no means 'very large' primes.
When I say very large, I really mean very large, something like:
4369518557955514614435635868603803074368490343736...548163288969925913941393434090233759524802729.
These numbers can have more than 300 digits!
The numbers I chose were only for clear exposition (and to be able to write them down!).
To put this in perspective: if you tried to guess one of these 300-digit prime factors by checking one billion numbers every second, it would take you longer than the age of the universe to find it!
Where You Use This Every Day
You might not realize it, but you rely on RSA encryption dozens of times each day:
Online Shopping: Every time you enter your credit card information, RSA protects it from hackers
Banking: Your online banking sessions are secured using these mathematical principles
Messaging: Apps like WhatsApp use modern versions of public key cryptography to protect your conversations
Email: Gmail, Outlook, and other email services encrypt your messages in transit
Software Updates: Even downloading apps or system updates relies on these keys to verify authenticity
The Future Challenge
There's a catch to this seemingly perfect system: quantum computers.
While today's computers would take billions of years to crack RSA encryption, a sufficiently powerful quantum computer could potentially do it in hours or days. That's why cryptographers are already working on "quantum-resistant" encryption methods—but that's a story for another newsletter!
The Beauty of Cryptography
The next time you buy something online or check your bank account, remember that you're witnessing one of mathematics' most elegant solutions to an ancient problem. What started as a theoretical breakthrough in the 1970s now protects trillions of dollars and billions of private conversations every day.
The beauty of public key cryptography lies in its simplicity: anyone can lock the box, but only you can open it. It's a mathematical trick that turned the impossible into the everyday, proving once again that sometimes the most profound innovations come from the most elegant ideas.
And the best part? The math that makes it work is literally public—yet remains unbreakable by design.
