The Art of Mental Math: Patterns, Shortcuts, and Intuition
Simple Tricks that Train your Brain to See Numbers Differently
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
Imagine you’re at a store and see a phone that costs 700€. You manage to get a 15% discount—how much are you saving?
If you reach for your calculator, you are not alone. Most of us do. But what if you could calculate it in your head—fast, confidently, and even enjoy it?
Mental math isn’t about showing off or memorizing tables. It’s about learning to see numbers differently—spotting shortcuts and patterns that make calculations simple. Let’s explore a few tricks that will make math feel lighter, quicker, and surprisingly fun.
The Fast Way
The easiest way, of course, is to use a calculator.
Type in 0.15 × 700 and you’ll find out you’re saving 105€.
And honestly, I’d recommend this in most cases—if a calculator can do it for you, don’t waste brainpower! You’ll get a faster and more reliable answer.
But sometimes you don’t have a calculator—or you just want to sharpen your mental math. That’s when a few tricks come in handy.
The Back-Up Plan
Without a calculator, you could multiply 0.15 × 700 the usual way—by hand or on paper. It’ll work, but there’s a smarter way.
Let me share a few techniques I personally find useful.
1. Forget the Zeros
Whenever you multiply numbers ending in zeros, ignore the zeros first and add them back later.
Example: 25 x 20
25 x 20 → ignore the zero in 20 → 25 x 2 = 50 → add one zero back → 500.
This trick also works for larger numbers:
120 × 300 → compute 12 × 3 = 36 → add four zeros → 36,000.
2,380 × 200,000 → compute 238 × 2 = 476 → add six zeros → 476,000,000.
This reduces clutter and helps you focus on the meaningful digits.
2. Divide & Conquer (Multiplication)
Split big numbers into smaller, easier ones.
Example: 12 x 25
12 × 25
We can write 12 = 6 × 2, so 12 × 25 = 2 × (6 × 25) = 2 × 150 = 300.
Another version: when multiplying by 5, remember 5 = 10 ÷ 2.
Example: 5 x 44
5 × 44 → divide 44 by 2 = 22 → then multiply by 10 → 220.
3. Divide & Conquer (Addition)
You can do something similar with addition.
Example: 147 + 234
- Round both numbers slightly: 147 = 150 - 3, and 234 = 230 + 4.
- Now add (150 + 230) +(- 3 + 4).
- Put everything together 147 + 234 = 381.
Breaking numbers into round figures makes the mental math smoother and reduces mistakes.
4. The Distributive Power — Share Everything
Here’s the secret weapon: the distributive property.
It says that multiplying a sum is the same as summing the products:
Since adding is easier than multiplying, this property is gold.
Example: 12 x 25
- Write 12 = 10 + 2.
- (10 + 2) x 25 = (10 x 25) + (2 x 25) = 250 + 50 = 300.
Simple, right? This property lets you handle big numbers by breaking them into friendlier chunks.
Be Creative!
Once you get comfortable, you can start mixing tricks.
Example: 0.15 x 700
- Write 0.15 = 0.1 + 0.05.
- 0.1 x 700 = 70
- 0.05 x 700 = (0.1 x 70) / 2 = 35.
- Add them: 70 + 35 = 105.
Example: 34 x 90
- Forget the 0 in 90 → think of 34 x 9, and add a zero later.
- Write 34 = 30 + 4.
- 30 x 9 = 270
- 4 x 9 = 36.
- 270 + 36 = 306.
- Add the zero →3,060.
Example: 9 x 78
- Write 9 = 10 - 1
- 10 x 78 = 780.
- 1 x 78 = 78.
- Subtract → 702.
Conclusion
Mental math isn’t about doing everything by hand — it’s about understanding numbers well enough to play with them.
In fact, this is how we mathematicians do mental math. We’re not faster at multiplying digits one by one—we’re better at seeing structure: splitting numbers, spotting patterns, and using properties like the distributive rule. The secret isn’t speed—it’s strategy.
The shortcuts above not only make calculations faster; they build intuition. After a while, you’ll start to “see” numbers differently—round them, split them, recombine them—and realize that what once felt like arithmetic is really just pattern recognition.
So next time you get a discount, or split a bill, try one of these tricks. You might be surprised at how fast your brain catches up.



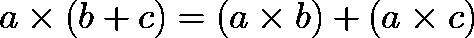



I'm in the process of self-education, after not having had the opportunity in youth. It are accessible articles as these that help people in my situation form that precious foundation. Thank you for writing this. I'm sure to follow your account.
Next time we go out for dinner, I’m using my brainpower to split the bill!! Not paying the whole check again! :)