The Strategy Behind Messi’s Penalty Kicks
Exploring the Connection Between Optimal Strategy and Randomization
This is The Curious Mind, by Álvaro Muñiz: a newsletter where you will learn about technical topics in an easy way, from decision-making to personal finance.
You are Leo Messi in the World Cup final.
The game has gone to penalties, and it’s your turn to kick. The world is watching you. You know you are better at kicking to the right, but you can’t always kick to the right if you want to maximise your chances of scoring.
Where do you kick the ball?
Today in a Nutshell
In some games, having a fixed strategy and a Nash equilibrium at the same time is impossible.
However, it is always possible to be in a Nash equilibrium: you just need to randomise your strategy (play A some percentage of the time, play B the rest).
Professional football players (probably without even knowing it) aim for a Nash equilibrium when kicking penalties.
Messi is a bit different…
Nash Equilibrium
Some weeks ago we discussed the Prisoner’s Dilemma and the best way to approach it.
We found that, unless there is cooperation, you should aim for a strategy that is in a Nash equilibrium:
A strategy is a Nash equilibrium if, given the opponent’s action, there is nothing you can do to improve your outcome (and the same goes for your opponent).
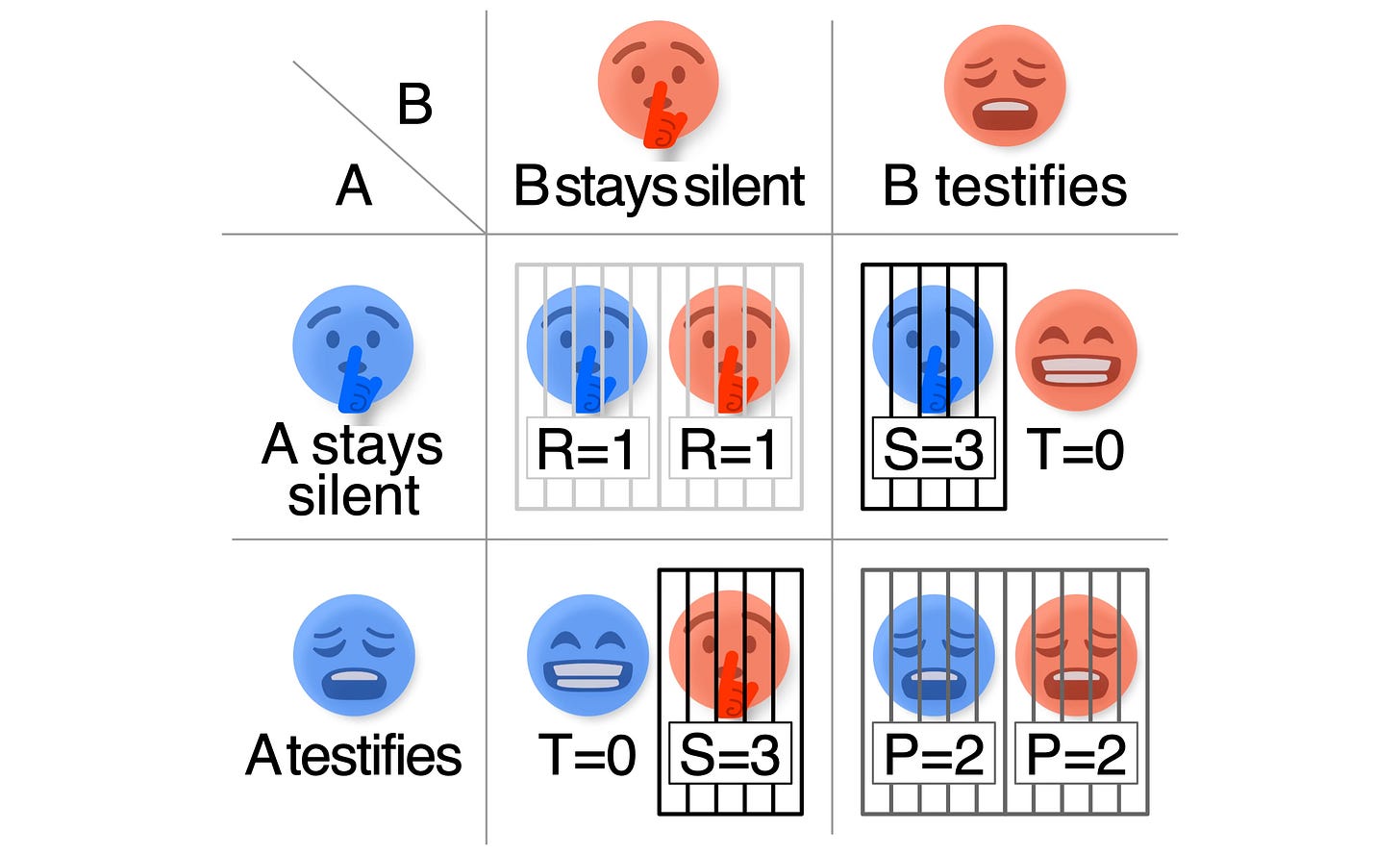
In the Prisoner’s Dilemma, each player has two options: to testify or to remain silent. The outcomes of these choices are summarised in the following cartoon:
If you stare at the cartoon for a bit, you will realise that there is a unique Nash Equilibrium: both players need to testify.
(For example, if A stays silent while B testifies, this is not a Nash Equilibrium: A can improve their situation by also testifying, reducing their sentence from 3 years to 1 year.)
Penalty Kicks
Let’s go back to the World Cup final, with you as Leo Messi.
Imagine that if the goalie guesses the side you are kicking to, they will always stop the ball. Also, assume that you always kick to one of the sides, never to the centre—this simplifies the exposition.
To turn the penalty kick into a strategy game, we need to assign numbers to represent ‘payoffs’ or ‘profit’. Here’s how we can do it:
If the goalie dives to the wrong side, it’s not automatically a goal: you can still miss. Since you are left-footed (you are Messi!), you’re better at kicking to the right. We can summarise this as follows:
If you kick to the right: you are more likely to score, so your payoff is +2.
If you kick to the left: you are less likely to score, so your payoff is +1.
The numbers (+1 and +2) simply reflect that it’s easier for you to score on your good side, even though the outcome (a goal) is the same in both cases.
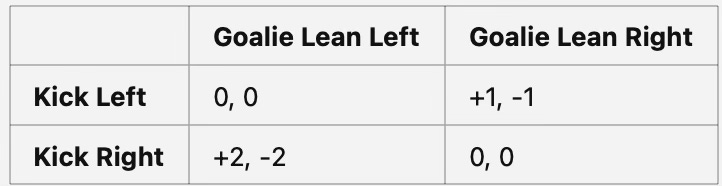
Now, let’s look for the Nash equilibrium:
Kick Left, Lean Left
Not a Nash Equilibrium. If the goalie leans left, the kicker can improve their payoff from 0 to +1 by kicking to the right.Kick Left, Lean Right
Not a Nash Equilibrium. If the kicker goes left, the goalie can improve their payoff from -2 to 0 by leaning left.Similarly, Kick Right, Lean Left and Kick Right, Lean Right are not Nash equilibria either.
Does this mean there is no Nash Equilibrium?
It doesn’t!
John Nash proved that in any game with a finite number of strategies, there is always a Nash equilibrium.
So how do we find it here?
Mixed Nash Equilibrium
No player consistently sticks to a single side in penalties.
If a kicker always goes to the right, the goalie can easily counter this by always leaning right. The same logic applies if the kicker always goes left. Instead, players alternate their strategies.
This is known as a mixed strategy:
A strategy is mixed if it involves some random component: we do Action A some percentage of the times, and Action B the rest.
For example, Messi kicks to the right about 70% of the time.
Is Messi doing his best by kicking to the right 70% of the time?
Finding the Nash Equilibrium
We already concluded that always kicking to one side is a bad idea. Instead, as the kicker, you will alternate between sides:
Kick to the right with some probability p (e.g., p = 70% for Messi).
Kick to the left the rest of the time (100 - p).
There are situations in life where your best option is to act random. Toss a coin, roll a dice…be unpredictable!
Here is something cool: there is a unique probability p that makes this game a Nash equilibrium. If you deviate from this p , the goalie can exploit your tendency.
Here’s how to find p:
If the goalie jumps left:
p% of the time you kick to the right, so the goalie gets a payoff of -2.
(100-p)% of the time you will kick to the left, and the payoff will be 0.
So, if the goalie jumps left, his average payoff is p x (-2) + (100 - p) x 0.
If the goalie jumps right:
p% of the time you kick to the right, so the goalie gets a payoff of 0.
(100-p)% of the time you will kick to the left, and the payoff will be -1.
So, if the goalie jumps right, his average payoff is p x 0 + (100 - p) x (-1).
If these payoffs are not the same, then the goalie will always lean to the most profitable side (otherwise, he would not be in a Nash equilibrium—every time he jumps to the least profitable side, he could be getting more profit by jumping to the other side). So, to get a Nash Equilibrium, we set both payoffs to be the same:
If you solve this, it says p = 33%.
What About Real-Life?
In a 2002 study, researchers found that professional players kick to their good side 45% of the time.
This is higher than the mathematically optimal 33%, but it is still remarkable: players kick to their bad side more often than to their good side.
Why? Because the goalie is more likely to lean toward the kicker’s good side!
The goalie knows the good side is more dangerous, so they position themselves there more frequently. To counteract this, the kicker intentionally kicks to their bad side more often.
This strategic adjustment leads to the Nash equilibrium, where the kicker goes to their good side 33% of the time, while the goalie jumps there 66% of the time. At this balance, neither the kicker nor the goalie can improve their chances by unilaterally changing strategies.
Rational Agents vs Real-Life Opponents
Now, math tells us 33%, but reality shows 45%. What’s going on?
Take Messi, for example. The best player in the world kicks to his right (his good side) 70% of the time—far above the theoretical 33%.
Does this mean math is wrong? Absolutely not.
The difference lies in how strategies work against imperfect opponents. In real life, goalies don’t play a mathematically optimal strategy—they aren’t “rational agents” who perfectly exploit the kicker’s tendencies.
Messi takes advantage of this: by observing that goalies fail to lean to his good side often enough, he can afford to kick there more frequently and still score.
In mathematical models, we assume all players are geniuses who always play optimally. But in real life, players make mistakes, and strategies can be exploited.
Your best strategy against a perfect opponent may differ from your best strategy against a flawed one.
Always ask yourself?
Who am I playing against? Are they playing optimally? If not, how can I exploit their weaknesses?



Amazing that you can use maths even for this 😱👏🏽