Financial Derivatives II–Options

The Sky is the Limit

This is MathMadeSimple, by Álvaro Muñiz: a newsletter where you will discover how math appears in every aspect of your life, from decision-making to personal finance.

---

In our first post we learned about one of the most common types of financial derivatives: futures. Today we will explore options: the chill cousin of futures.

🙇🏽‍♂️ Today in a nutshell

• Options give you the right, but not the obligation, to buy something in the future at a price which is fixed now (the ‘strike price’).

• The other party involved in the options contract has instead the obligation to sell (if you decide to buy).

• To make the game fair, to enter into an options contract you pay a fee. This fee depends on the strike price via the Black-Scholes equation.

• Uncertainty in the markets (volatility) makes an option more valuable. There is an unlimited upside potential, whereas the downside is limited.

🤝The obligation

If you have forgotten what financial derivatives and futures are, I got you:

A financial derivative is any type of financial contract whose value derives from another asset.

Our first example was a futures contract: a contract fixing now a price for some exchange in the future. It looked something like this:

I, the copper provider, commit to selling you 1 ton of copper at a price of $10/kg in one year’s time.

I, the business man, commit to buying from you 1 ton of copper at a price of $10/kg in one year’s time.

Signed by the copper provider and the business man.

In a futures contract there is an obligation, for both the buyer and the seller, to execute the exchange. They both commit to something, regardless of whether they end up feeling like it or not. None of them is in a better position than the other.

There is one and only one price at which that futures contract should be trading in the market: if the banks are offering you an interest rate of 2%, the price per kg should be

\(\$10 + (2\text{% of \$}10) = $10.2\)

(If you see any other price, buy it immediately and make free money!)

Two things can happen when you enter a futures contract:

• If the price of copper increases a lot this year and is higher than $10.2, your futures contract was a good deal. You saved money!

• But what if the price of copper is lower than $10.2 next year? What if it even decreased from its current price and trades at $9.5? Why did you commit to buying this?!

Here is where options come into play.

✋🏼 Don’t commit

An option gives you the right, but not the obligation, to buy something in the future at a price fixed now.

An options contract could look something like this:¹

I, the copper provided, commit to selling you 1 ton of copper at $11/kg in one year’s time—as long as you want to buy it from me.

Signed: the copper provider

There is a clear asymmetry between buyer and seller:

• The seller (the copper provider) is committing to something.

• The buyer (you) are just given the option to buy (if it is favorable to you).

A (call) option gives the buyer the option to buy an asset, while the seller has an obligation.

🤑 So…free money?

If you are thinking about free money, you got the game.

Such a contract would be too good for the buyer.

Say you are a buyer and can enter an options contract to buy 1 ton of copper in one year’s time at $11/kg.

• If in one year’s time the price is higher than $11/kg, you exercise your call option and use your right to buy at $11/kg. You immediately go to the market and sell that ton of copper at the higher market price, keeping the profit.

• If in one year’s time the price is lower than $11/kg, you decide that price is not good for you and don’t exercise your option. You had the right, not the obligation!

Regardless of what happens with the price of copper, you made money. This is free money.

Unfortunately for you and I, financial markets are not that flawed.

📈 The price of an option

To enter an options contract that gives you the right, but not the obligation, to buy 1 ton of copper in a year’s time at $11/kg, you will pay a fee (a ‘premium’).

Remember that before there were two things that could happen:

• If the future price is higher than $11/kg, you will exercise your option and buy at $11/kg. The buyer will have to sell it you at that price, even though the market is trading higher and he would prefer to sell it at that higher price.

• If the price is lower than the strike price, you will not exercise your option: you don’t have to!

Now that you pay a fee, even if the first case, you might not be making money. You might even be loosing money.

If next year copper trades at $13/kg and you have the option to buy at $11/kg, it seems as if you just made (and the seller just lost) $2. But what if the fee you payed for the option was $4? Then overall you are making $2 - $4 = -$2—and the seller is making money.

Before you would always win, and the seller would always loose. Now it all depends on what this fee is.

To have the right, but not the obligation, to buy something in the future at a particular price, you pay a fee to the seller.

Something very interesting happens with this fee.

In a futures contract, the only variable was the price at which we would do the exchange in the future. We saw here that we had to fix this price: any other price would allow investors to make free money.

In an options contract, we can fix any price for the exchange in the future—all we have to do is fix a corresponding fee.

It turns out that, given any strike price (the price for the exchange in the future), there is a unique option price (a unique fee) that does not allow the possibility of making free money.

🟰 The Black-Scholes equation

Finding such a price is a difficult problem in mathematics. Fischer Black, Myron Scholes and Robert Merton developed a partial differential equation that gives the unique fee for an option that does not allow the opportunity of free money.² It involves solving this little beast:

\(\left\lbrace \begin{array}{l} \frac{\partial V}{\partial t} + \frac{1}{2} \sigma^2 S^2 \frac{\partial^2 V}{\partial s^2} + r S \frac{\partial V}{\partial S} - rV = 0 \\ V(T,s) = K(s) \quad \forall s \end{array} \right. \qquad \qquad \text{Black-Scholes equation}\)

If your head is hurting, I don’t blame you.

To really understand what a solution should look like, mathematicians often study limit cases.

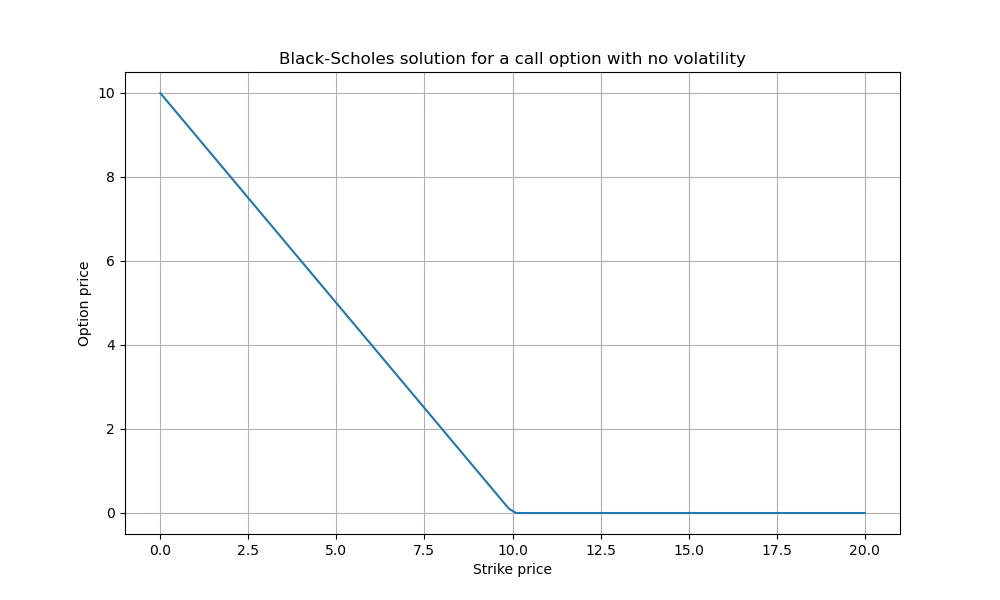
For instance, suppose that, for some reason, you knew that the price of copper could not change at all. In financial jargon, you would say that the volatility is zero.

Let’s also assume the interest rate offered by banks is zero.

What would be the fair price of an option under this assumption?

• If the strike price is higher than the current price ($10), the option value is zero. Think about it like this: if you are certain that the price will not change, why would you pay for an option that gives you the right to buy at a higher price in the future? It will never benefit you, it’s worthless!

• If the strike price is lower than the current price, the option starts gaining value. How much value does it gain? Say the strike price is $8. You know for a fact that the current price will not move (we are assuming no volatility). So when the time comes to exercise your option, you will be able to buy copper for $8, while in the market it will still be trading at $10. You are making $2 of profit, so that’s the price it should have now (otherwise, free money!).

The graph below shows what would be the fair price of an option if there were no volatility, assuming the current price of copper in the market is $10:

Of course, every asset has some volatility. But the example above is extremely useful to think about the general case.

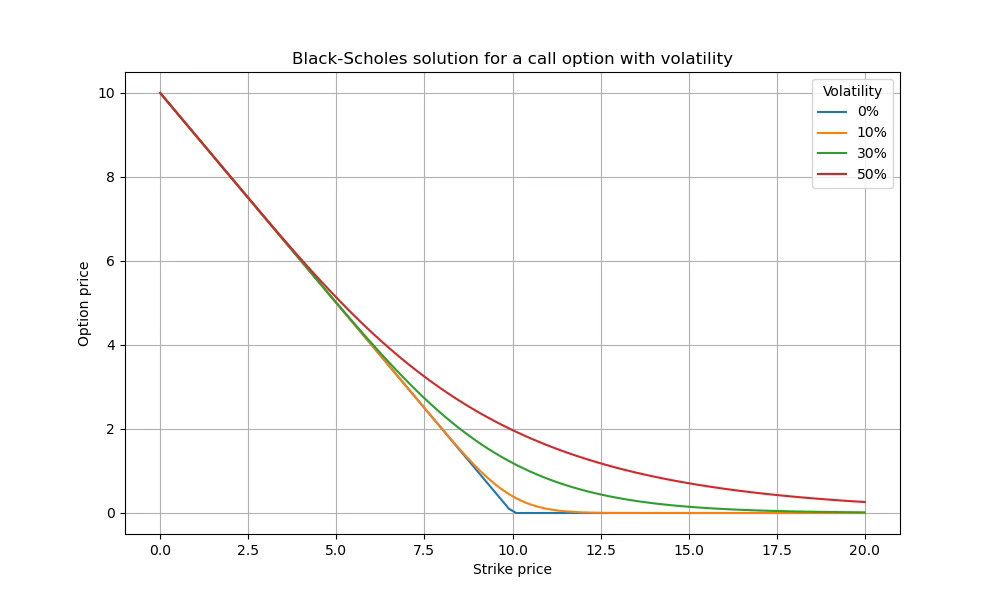
To understand what happens when there is volatility, you should think qualitatively instead of quantitatively. Don’t think about exact numbers, think about general behaviour.

How should the volatility affect the price of the option?

• If the strike price is higher than the current price, before the option was worthless. Now the price can rise higher than the strike price, so that you will have made money with your option.
  Before it was always worthless, whereas now it might be valuable. You will make at least as much money as before.

• If the strike price is lower than the current price, the situation is a bit more tricky. With no volatility, the pay-off of the option was fixed. Now two things can happen: the price of copper increases, so that you make more money than before; or it decreases, so that you make less money. It’s not clear if volatility helps or not now.
  The key here is an asymmetry. The worst that can happen is that the price goes down lower than the strike price, so that you loose whatever fee you payed (a fixed amount). On the other hand, the upside potential is unlimited: the price doesn’t have an upper limit. This makes the option be more valuable now than before.

The graph below shows the only fair price for an option to buy an copper at a given strike price in one year’s time, if copper is currently trading at $10.

The upshot is:

Volatility increases the value of an option.

Your winning potential is now unlimited—you must pay for it.

🆕 In future editions…

• How are options and futures actually used by investors.

• The risk-neutral measure: a fake version of reality where investors are not risk-averse but price make more sense.

• How to use the ideas of option pricing to forecast elections.

🤔 Can’t wait to learn more?

• Investopedia is a great resource for finance-related concepts

• Your dear friend Wikipedia.

❓A question for you:

How should the graphs above change if the interest rate offered by banks were not zero?

Remember the strategy: we want to avoid the possibility of making free money.

1. The option below is usually called a call option: it gives the buyer the option to buy, while the seller has an obligation. An option giving the buyer the obligation to buy and the seller the option to sell is called a put option.

2. Merton and Scholes received the Nobel Prize in Economics for this discovery.